Wärmekraftmaschinen

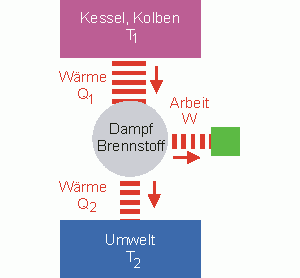
Verbrennungsmotoren als typisches Beispiel

Joachim Herz Stiftung

Typische Beispiele für Wärmekraftmaschinen sind Dampfmaschinen oder Verbrennungsmotoren, egal ob Bezin- oder Dieselmotor, Zwei oder Viertakter. Wärmekraftmaschinen dienen dazu, mechanische Arbeit zu leisten. Um dies zu erreichen, nutzen Wärmekraftmaschinen immer eine Temperaturdifferenz \(\Delta T\) zwischen zwei unterschiedlichen Reservoirs und das Bestreben von Wärme aus, vom Reservoir höherer Temperatur zum Reservoir mit niedrigerer Energie zu fließen. Die Reservoirs können dabei z.B. der Dampfkessel und die Umwelt sein.

Funktionsweise

Das Funktionsprinzip kannst du allgemein folgendermaßen beschreiben: Durch die Abkühlung des heißen Reservoirs der Temperatur \(T_1\)  kann mechanische Arbeit \(W\) verrichtet werden. Dabei wird jedoch die dem heißen Reservoir entzogene Wärmeenergie \(Q_1\) nicht vollständig in mechanische Arbeit \(W\) umgewandelt. Ein Teil, nämlich die Wärmemenge \(Q_2\), wird als Abwärme an das kältere Reservoir mit der Temperatur \(T_2\) abgegeben und erwärmt dieses.

Joachim Herz Stiftung

Wirkungsgrad

Eine wirkungsvolle (effiziente) Wärmekraftmaschine wandelt einen möglichst großen Teil der Wärmeenergie \(Q_1\) in mechanische Arbeit \(W\) um. Mathematisch kannst du dies mithilfe des sog. Wirkungsgrads \(\eta\) beschreiben. Bei Wärmekraftmaschinen ist \[\eta=\rm{\frac{nutzbare~Arbeit}{aufzuwendende~Wärmemenge}}=\frac{W}{Q_1}\]

Dabei gilt grundsätzlich, dass periodisch arbeitende Wärmekraftmaschinen die zugegeführte Wärmemenge \(Q_1\) nicht vollständig in mechanische Arbeit umwandeln können. Es entsteht immer Abwärme. Daher ist bei einer Wärmekraftmaschine  immer \(\eta < 1\).

Kältemaschine und Wärmepumpe

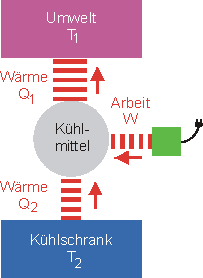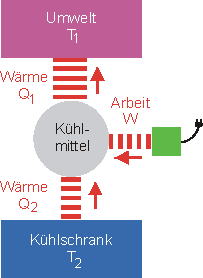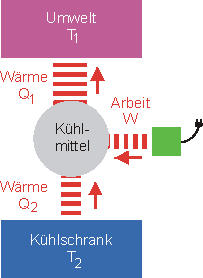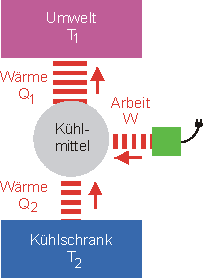
Bei Kältemaschinen und Wärmepumpen laufen die Prozesse in umgekehrter Richtung ab. Durch das Verrichten von Arbeit wird Wärme von einem kalten zu einem warmen Reservoir transportiert. 

Kältemaschine (Kühlschrank, Klimaanlage)	Wärmepumpe
Ziel: Von einem kalten Reservoir der Temperatur \({{T_2}}\) soll eine Wärmemenge \(Q_2\) abtransportiert werden. Dazu ist die mechanische Arbeit \(W\) nötig. Dieser Prozess ist stets mit der Wärmezufuhr \(Q_1\) an ein wärmeres Reservoir (Temperatur \({{T_1}}\)) verbunden.	Ziel: Die Temperatur \({{T_1}}\) eines Zimmers soll erhöht werden indem ihm die Wärmemenge \(Q_1\) zugeführt wird. Dazu ist die mechanische Arbeit \(W\) notwendig, die dem kälteren Reservoir der Temperatur \({{T_2}}\) (der Umwelt) Wärme entzieht und zum warmen Reservoir transportiert.
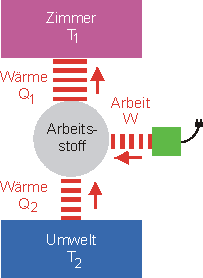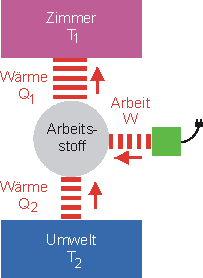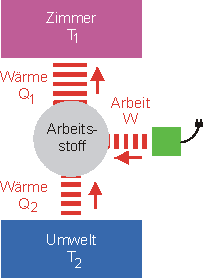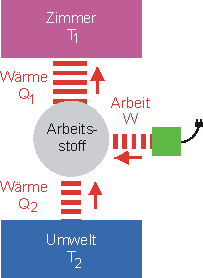Nutzenergie: \({{Q_2}}\) Aufzuwendende Arbeit: \(W\) \[\eta  = \frac{{{Q_2}}}{W}\]	Nutzenergie: \({{Q_1}}\) Aufzuwendende Arbeit: \(W\) \[\eta  = \frac{{{Q_1}}}{W}\]