Prinzip der Absorption
Ein Atom kann beim Aufeinandertreffen mit einem Photon Energie aufnehmen und dadurch in einen angeregten Energiezustand gelangen. Das Photon existiert danach nicht mehr. Einen solchen Vorgang bezeichnen wir als Absorption.
Das Prinzip einer solchen Absorption zeigt die Animation in Abb. 1. In der Mitte siehst du ein ruhendes Atom mit seinen verschiedenen Energiezuständen. Das Atom befindet sich zu Beginn im Grundzustand mit der Energie \(E_1\).
Wenn du die Animation startest, erkennst du ein Photon, dass sich auf das Atom zubewegt.
Wenn das Photon auf das Atom trifft, geht seine gesamte Energie auf das Atom über. Das Atom nimmt die Energie \(\Delta E_{12}\) auf und geht dadurch vom Grundzustand mit der Energie \(E_1\) in den angeregten Energiezustand mit der Energie \(E_2 = E_1 + \Delta E_{12}\) über.
Das Photon existiert nach der Energieübergabe nicht mehr.
Abhängigkeit des Prozesses von der Energie \(E_{\rm{Ph}}\) des Photons
Beim Aufeinandertreffen eines Atoms im Grundzustand mit einem Photon können in Abhängigkeit von der Energie \(E_{\rm{Ph}}\) des Photons verschiedene Fälle auftreten:
\(E_{\rm{Ph}} < \Delta E_{12}\)
Ist die Energie \(E_{\rm{Ph}}\) des Photons kleiner als die Energiedifferenz \(\Delta E_{12}\) zwischen Grundzustand und erstem angeregten Zustand des Atoms, so geschieht keine Absorption. Das Photon gibt keine Energie an das Atom ab, so dass das Atom im Grundzustand bleibt. Das Photon bewegt sich nach dem Aufeinandertreffen mit gleicher Energie weiter.
\(E_{\rm{Ph}} = \Delta E_{12}\)
Ist die Energie \(E_{\rm{Ph}}\) des Photons genau so groß wie die Energiedifferenz \(\Delta E_{12}\) zwischen Grundzustand und erstem angeregten Zustand des Atoms, so wird das Photon absorbiert. Die gesamte Energie des Photons geht auf das Atom über, so dass das Atom in den ersten angeregten Energiezustand übergeht. Das Photon existiert danach nicht mehr.
\(\Delta E_{12} < E_{\rm{Ph}} < \Delta E_{13}\)
Ist die Energie \(E_{\rm{Ph}}\) des Photons größer als die Energiedifferenz \(\Delta E_{12}\) zwischen Grundzustand und erstem angeregten Zustand, aber kleiner als die Energiedifferenz \(\Delta E_{13}\) zwischen Grundzustand und zweitem angeregtem Zustand, so geschieht keine Absorption. Das Photon gibt keine Energie an das Atom ab, so dass das Atom im Grundzustand bleibt. Das Photon bewegt sich nach dem Aufeinandertreffen mit gleicher Energie weiter.
\(E_{\rm{Ph}} = \Delta E_{13}\)
Ist die Energie \(E_{\rm{Ph}}\) des Photons genau so groß wie die Energiedifferenz \(\Delta E_{13}\) zwischen Grundzustand und zweitem angeregten Zustand des Atoms, so wird das Photon absorbiert. Die gesamte Energie des Photons geht auf das Atom über, so dass das Atom in den zweiten angeregten Energiezustand übergeht. Das Photon existiert danach nicht mehr.
\(E_{\rm{Ph}} = \Delta E_{1\infty}\)
Ist die Energie \(E_{\rm{Ph}}\) des Photons genau so groß wie die Ionisationsenergie \(\Delta E_{1\infty}\), so wird das Photon absorbiert. Die gesamte Energie des Photons geht auf das Atom über, so dass das Atom ionisiert wird, also ein Elektron aus der Atomhülle verliert und einfach positiv geladen ist. Das Photon existiert danach nicht mehr.
\(\Delta E_{1\infty} < E_{\rm{Ph}}\)
Ist die Energie \(E_{\rm{Ph}}\) des Photons größer als die Ionisationsenergie \(\Delta E_{1\infty}\), so wird das Photon absorbiert. Die gesamte Energie des Photons geht auf das Atom über, so dass das Atom ionisiert wird, also ein Elektron aus der Atomhülle verliert und einfach positiv geladen ist. Da die Energie des Photons größer als die Ionisationsenergie des Atoms ist, geht die restliche Energie des Photons in kinetische Energie des Elektrons über. Das Elektron bewegt sich dann mit dieser kinetischen Energie vom Atom weg. Das Photon existiert danach nicht mehr.
Absorption
Wenn ein Atom mit einem (passenden) Photon zusammentrifft, kann es die Energie des Photons aufnehmen und vom Grundzustand in einen angeregten Zustand übergehen oder sogar ionisiert werden. Das Photon wird bei diesem Prozess, den man Absorption nennt, vernichtet; es existiert nachher nicht mehr.
Für eine Anregung eines Atoms, das sich im Grundzustand befindet, muss die Energie \(E_{\rm{Ph}}\) des Photons genau gleich der Energiedifferenz \(\Delta E_{1m}\) von Grundzustand und einem angeregten Zustand des Atoms sein.
Für eine Ionisation eines Atoms, das sich im Grundzustand befindet, muss die Energie \(E_{\rm{Ph}}\) des Photons größer oder genau gleich der Ionisationsenergie \(\Delta E_{1\infty}\) des Atoms sein.
Beobachtung der Absorption beim Versuch zur Resonanzabsorption von Natrium
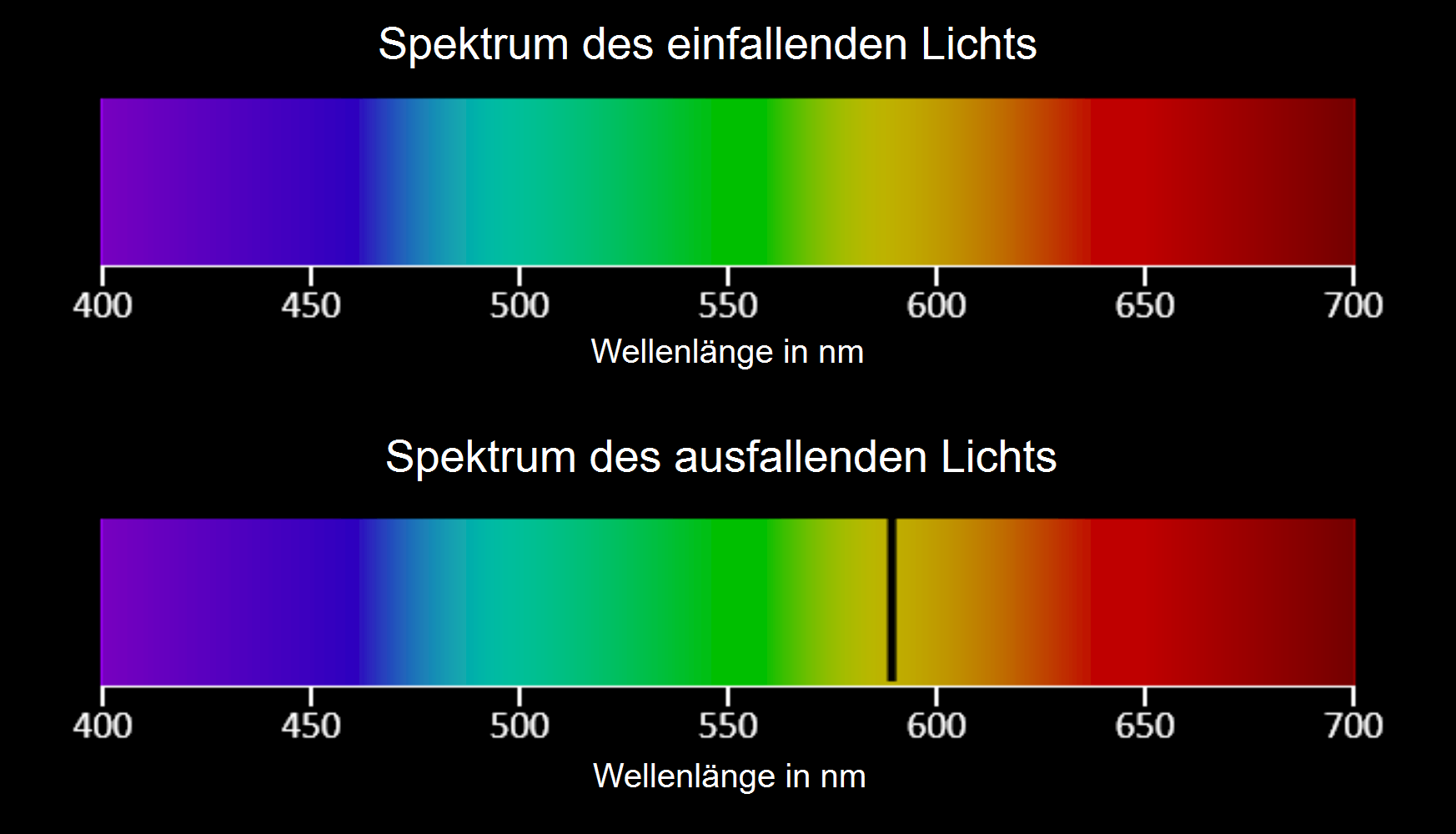
Beim Versuch zur Resonanzabsorption von Natrium durchläuft das Licht z.B. einer Kohlebogen- oder Halogenlampe eine Glasröhre, die mit Natrium (\(\rm{Na}\))-Dampf gefüllt ist. Das einfallende und das ausfallende Licht werden spektral zerlegt. Das Diagramm in Abb. 3 zeigt die Spektren des einfallenden (oben) und des ausfallenden (unten) Lichts.
Das untere Spektrum unterscheidet sich vom oberen durch das Fehlen von Licht im gelben Bereich des Spektrums. Dieses gelbe Licht hat eine Wellenlänge von ca. \(590\,\rm{nm}\), die Photonen also ein Energie von ca. \(2{,}1\,\rm{eV}\). Diese Energie entspricht exakt der Energiedifferenz \(\Delta E_{12}\) zwischen dem Grundzustand und dem ersten Anregungszustand von \(\rm{Na}\).
Somit können die Photonen mit entsprechender Wellenlänge bzw. Energie von den \(\rm{Na}\)-Atomen absorbiert werden. Dabei gehen die \(\rm{Na}\)-Atome in den ersten Anregungszustand über und die Photonen werden vernichtet.
Im ausfallenden Licht fehlen nun diese Photonen, was im Spektrum des ausfallenden Lichts durch eine Lücke im gelben Bereich deutlich wird.
Photonen mit anderen Wellenlängen bzw. Energien können die \(\rm{Na}\)-Atome nicht anregen, da ihre Energien nicht mit Anregungsenergien des \(\rm{Na}\) übereinstimmen. Sie durchlaufenn deshalb das \(\rm{Na}\)-Gas und sind im Spektrum des ausfallenden Lichts beobachtbar.
Hinweis: Es wird hier sowohl vernachlässigt, dass es sich um eine Doppellinie handelt, als auch die Existenz weiterer Linien im Absorptionsspektrum von \(\rm{Na}\).