Zum Einstieg in das Thema "Induktion durch Änderung des Magnetfeldes" werden meist Anordnungen betrachtet, bei denen die Feldspule (in ihr wird das Magnetfeld verändert) und die Induktionsspule (in ihr wird die induzierte Spannung festgestellt) zwei verschiedene Anordnungen waren. Wie die Experimente zur Selbstinduktion aber zeigen, tritt ein Induktionseffekt beim Ein- und Ausschalten des Stromes in der Feldspule selbst auf. In diesem Fall spricht man von Selbstinduktion.
Unter Selbstinduktion versteht man die Induktionswirkung eines Stromes auf seinen eigenen Leiterkreis:
-
Ändert sich der durch eine Spule fließende Strom (z.B. beim Ein- und Ausschalten), so bewirkt dieser eine Änderung des magnetischen Flusses durch die "eigene" Spule.
-
Aufgrund des Induktionsgesetzes tritt eine Induktionsspannung auf, die nach LENZ die Ursache ihrer Entstehung zu hemmen sucht.
-
Dadurch steigt der Strom beim Einschalten einer Spule erst allmählich auf seinen stationären Endwert. Beim Ausschalten der Spule kann der Strom noch "nachfließen", wenn ein entsprechender Stromkreis zur Verfügung steht.
_Bild.gif)
Für die induzierte Spannung \(U_{\rm{i}}\) z.B. in einer langen luftgefüllten Zylinderspule mit der Windungszahl \(N\), der Länge \(l\) und einer Querschnittsfläche vom Inhalt \(A\) gilt\[\begin{eqnarray}{U_{\rm{i}}} &=& - N \cdot \frac{{d\Phi }}{{dt}}\\ &=& - N \cdot A \cdot \frac{{dB}}{{dt}}\\ &=& - N \cdot A \cdot \frac{{d\left( {{\mu _0} \cdot \frac{N}{l} \cdot I} \right)}}{{dt}}\\ &=& - N \cdot A \cdot {\mu _0} \cdot \frac{N}{l} \cdot \frac{{dI}}{{dt}}\\ &=& - {\mu _0} \cdot \frac{{A \cdot {N^2}}}{l} \cdot \frac{{dI}}{{dt}}\end{eqnarray}\]und allgemein\[U_{\rm{i}} \sim - \frac{dI}{dt}\]Dies bedeutet, dass der Betrag der induzierten Spannung proportional zur Steigung der \(t\)-\(I\)-Kurve ist (vgl. die nebenstehende Veranschaulichung).
Spulenformel und Definition der Induktivität
Untersucht man experimentell oder theoretisch den Zusammenhang zwischen der Änderungsrate \(\frac{dI}{dt}\) der Stärke des Stroms, der durch eine Spule fließt, und der Spannung \(U_{\rm{i}}\), die in der Spule induziert wird, dann ergibt sich:
Die Spannung \(U_{\rm{i}}\) ist proportional zur Änderungsrate \(\frac{dI}{dt}\)\[U_{\rm{i}}= - L \cdot \frac{dI}{dt} \quad(1)\]Den Proportionalitätsfaktor \(L\) bezeichnet man als Induktivität der Spule (lat.: inductio, Einführung). Die Induktivität hat für verschiedene Spulen unterschiedliche Werte und ist von der Geometrie der Spule und der Permeabilität des Materials in der Spule abhängig.
Für die Einheit der Induktivität gilt wegen \((1)\) und \(\left|U_{\rm{i}}\right| =L \cdot \frac{dI}{dt} \Leftrightarrow L = \frac{\left| U_{\rm{i}} \right|}{\frac{dI}{dt}}\)\[\left[ L \right] = \frac{\left[ \left|U_{\rm{i}}\right| \right]}{\left[ \frac{dI}{dt} \right]} = \frac{1\,\rm{V}}{1\,\frac{\rm{A}}{\rm{s}}} = 1\,\frac{\rm{V}\,\rm{s}}{\rm{A}} =:1\,\rm{H}\;\rm{(Henry)}\]
Eine Spule besitzt also die Induktivität \(1\,\rm{H}\), wenn bei einer Änderungsrate der Stromstärke von \(1\,\frac{\rm{A}}{\rm{s}}\) in der Spule eine Spannung von \(1\,\rm{V}\) induziert wird.
| Größe | ||
| Name | Symbol | Definition |
| Induktivität | \(L\) | \(L := \frac{\left| U_{\rm{i}} \right|}{\frac{dI}{dt}}\) |
| Einheit | ||
| Name | Symbol | Definition |
| Henry | \(\rm{H}\) | \(1\,\rm{H}:=1\,\frac{\rm{V}\,\rm{s}}{\rm{A}}\) |

Joseph HENRY (1797 - 1878)
von T. W. Smillie (1843-1917) [Public domain], via Wikimedia Commons
In Erinnerung an den amerikanischen Physiker Joseph HENRY (1797 - 1878), der sich große Verdienste bei der Erforschung der elektromagnetischen Induktion erwarb, wird die Einheit der Induktivität als 1 Henry bezeichnet.
Ober- und Untereinheiten
Die Induktivität der meisten Spulen ist wesentlich kleiner als \(1\,\rm{H}\). Um kleinere Induktivitäten bequem beschreiben zu können, führt man Untereinheiten der Induktivität ein. Die gebräuchlichsten sind\[1\,\rm{\mu H}=\frac{1}{1\,000\,000}\,\rm{H}=1\cdot 10^{-6}\,\rm{H}\]\[1\,\rm{nH}=\frac{1}{1\,000\,000\,000}\,\rm{H}=1\cdot 10^{-9}\,\rm{H}\]
Konsequenzen der Selbstinduktivität
Einschaltvorgang
- Der Strom geht nicht sofort auf seinen stationären Endwert \({I_0} = \frac{U_0}{R}\), sondern steigt allmählich auf diesen Endwert an.
- Mit dem Stromanstieg ist eine Zunahme des magnetischen Flusses in der Spule verbunden: \(\frac{{d\Phi }}{{dt}} > 0\).
- Die Flussänderung ruft eine induzierte Spannung \({U_{{\rm{i}}}}\) hervor, die (nach der Regel von LENZ) der von außen angelegten Spannung \(U_0\) entgegengerichtet ist. Die an der idealen Spule \(L\) anliegende Spannung \({U_{{\rm{L}}}}\) ist gegengleich zu dieser Induktionsspannung.
Ausschaltvorgang
- Der Strom geht nicht sofort auf Null zurück, sondern sinkt allmählich auf Null ab.
- Mit dem Stromabfall ist eine Abnahme des magnetischen Flusses in der Spule verbunden: \(\frac{{d\Phi }}{{dt}} < 0\).
- Die Flussänderung ruft eine induzierte Spannung \({U_{{\rm{i}}}}\) hervor, die die aufgrund des Induktionsgesetzes in differentieller Form positiv ist.
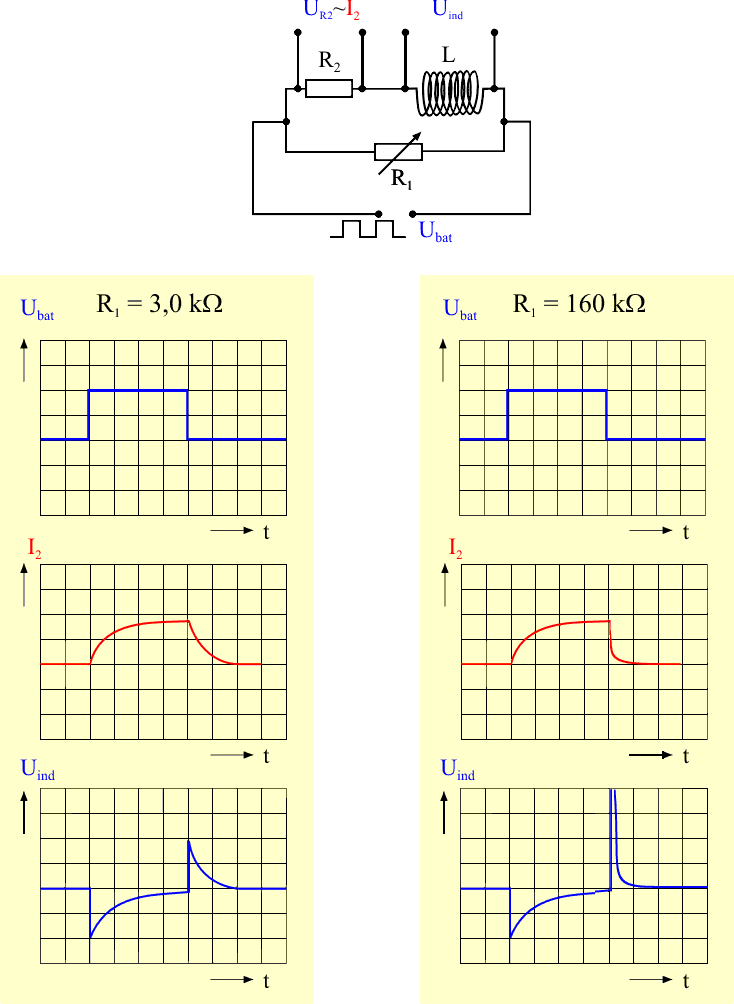
Eine nähere Betrachtung des Ein- und Ausschaltvorganges bei einer Spule kann mit Hilfe von Oszilloskopbildern durchgeführt werden (auch dies ist eher für besonders Interessierte gedacht).