Gelangt eine Schallwelle an das Ohr, so bringt sie das Trommelfell zum Schwingen. Durch komplizierte Vorgänge im Ohr und unserem Gehirn haben wir dann einen Höreindruck. Im Physikunterricht verwendet man als Schallquelle oft einen Lautsprecher, welcher durch einen Sinusgenerator angeregt wird.
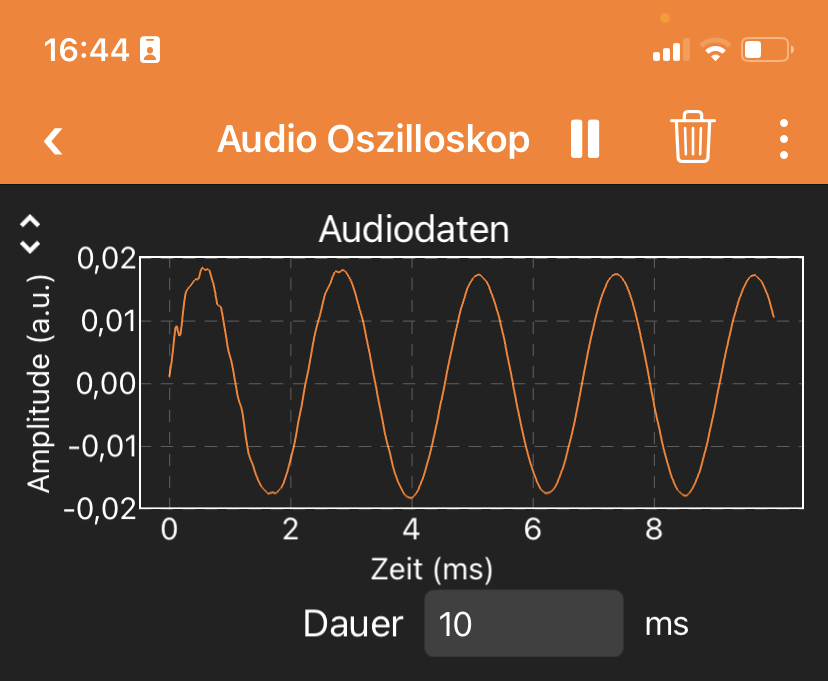
Als Empfänger kannst du ein Smartphone mit der App phyphox nutzen (Abb. 1). Die Funktion "Audio Oszilloskop" stellt Töne grafisch dar.
Durch Erhöhung der Frequenz der ausgesandten Schallwelle (man erkennt dies z.B. am Schirmbild des Oszilloskops bzw. an der Einstellung des Sinusgenerators) steigt die Höhe des Tons. Erhöht man die Amplitude der den Lautsprecher anregenden elektrischen Schwingung, so steigt die Lautstärke des vom Lautsprecher ausgesandten Signals. Die Ausschläge am Oszilloskop wachsen an.
Dass die Frequenz der Schallwelle die vom Empfänger registrierte Tonhöhe bestimmt, war zunächst keine gesicherte Tatsache in der Physik. Der Zusammenhang zwischen Tonhöhe und Frequenz wurde von August Seebeck im 19. Jahrhundert mit einer Lochsirene zweifelsfrei nachgewiesen. Auf konzentrischen Kreisen sind bei ihr von innen nach außen 24, 27, 30, 32, 36, 40, 45 und 48 Löcher in jeweils gleichem Abstand angebracht, durch welche der Luftrom durchtreten kann.
- Steigert man die Winkelgeschwindigkeit der Scheibe, so nimmt die Höhe des hörbaren Tons zu.
- Bläst man mit der Düse die Lochkreise der Reihe nach von innen nach außen an, so hört man eine Dur-Tonleiter. Der Eindruck einer Dur-Tonleiter bleibt auch erhalten, wenn man die Drehfrequenz der Scheibe erhöht.
Der Kammerton \(\bar a\) wurde im Jahre 1939 auf 440 Hz festgelegt. In der folgenden Tabelle sind die Frequenzen und die Frequenzverhältnisse der Töne der C-Dur-Tonleiter in reiner Stimmung, sowie deren Position in einer Notenzeile dargestellt.
| Ton | \(\bar c\) | \(\bar d\) | \(\bar e\) | \(\bar f\) | \(\bar g\) | \(\bar a\) | \(\bar h\) | \(\bar {\bar c}\) |
|---|---|---|---|---|---|---|---|---|
| Frequenz in Hz | 264 | 297 | 330 | 352 | 396 | 440 | 495 | 528 |
| relatives Frequenz- verhältnis |
\(1\) | \(\frac{9}{8}\) | \(\frac{5}{4}\) | \(\frac{4}{3}\) | \(\frac{3}{2}\) | \(\frac{5}{3}\) | \(\frac{15}{8}\) | \(2\) |
| Intervall bezüglich des Grundtons \(\bar c\) |
Prim | Sekund | Terz | Quart | Quint | Sext | Septim | Oktav |
Aufgabe
Zeigen Sie, dass beim Anblasen der äußersten Lochreihe mit 48 Löchern der entstehende Ton die doppelte Frequenz hat, wie beim Anblasen der innersten Reihe mit 24 Löchern.
Berechnen Sie, mit welcher Frequenz die Scheibe rotieren muss, damit die Lochreihe mit den 48 Löchern den Kammerton \(\bar a = 440\,\rm{Hz}\) hervorbringt.