Akustische Phänomene

Reflexion von Schallwellen (Echo)

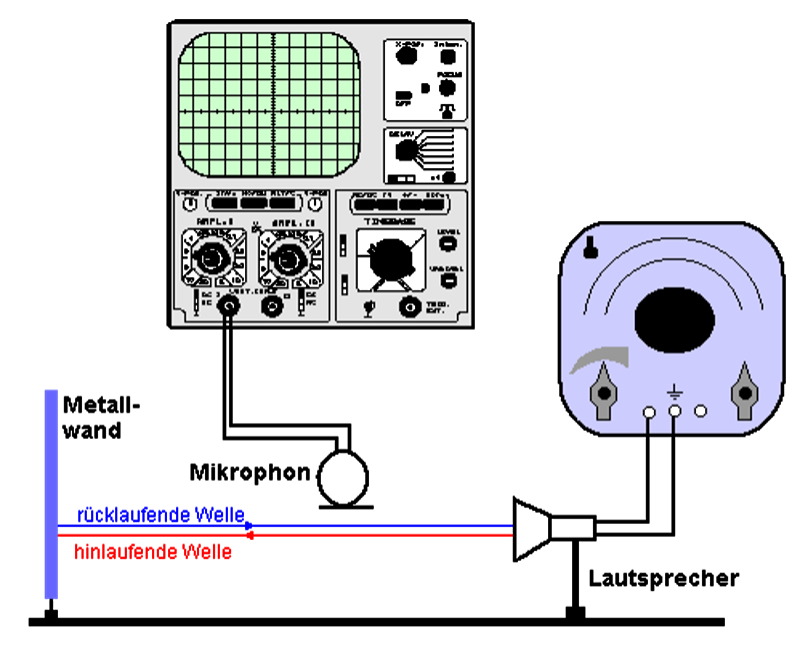
Da Schallwellen an glatten Wänden (vgl. Echo vom Königssee) reflektiert werden, kann man mit dem unten skizzierten Versuch eine zur Metallwand hinlaufenden Welle (rot) eine rücklaufende Welle (blau) erzeugen. Da diese beiden Wellen gleiche Frequenz und vor der Wand vergleichbare Amplitude besitzen, kann man insbesondere vor der Metallwand eine gut ausgeprägte stehende Schallwelle feststellen (vgl. hierzu auch das Grundwissen über Wellen). Der Nachweis der Knoten und Bäuche der stehenden Schallwelle erfolgt durch das Mikrophon.

Variiert man nun die Frequenz der vom Lautsprecher ausgesandten Schallwelle, so kann man stets stehende Wellen vor der Wand beobachten, jedoch ändert sich mit der Frequenz der Abstand benachbarter Knoten.

Ausbildung einer stehenden Welle

Bei dem obigen Versuch passierte eine Reflexion der Schallwelle an der Metallwand. Die blau skizzierte rücklaufende Welle wird am kleinen Lautsprecher nicht nennenswert reflektiert, sie läuft zum großen Teil am Lautsprecher vorbei nach rechts.
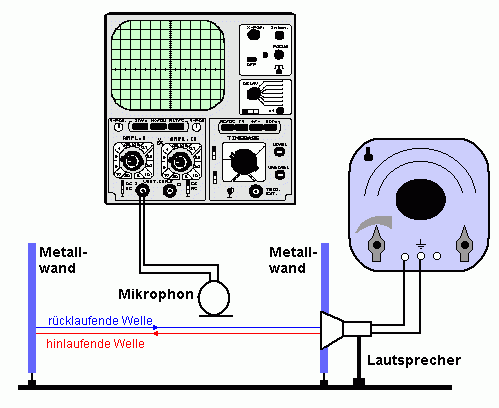
Ein deutlich anderes Ergebnis erhält man, wenn durch eine zweite Platte am Ort des Lautsprechers dafür gesorgt wird, dass auch hier deutliche Reflexionen auftreten können.

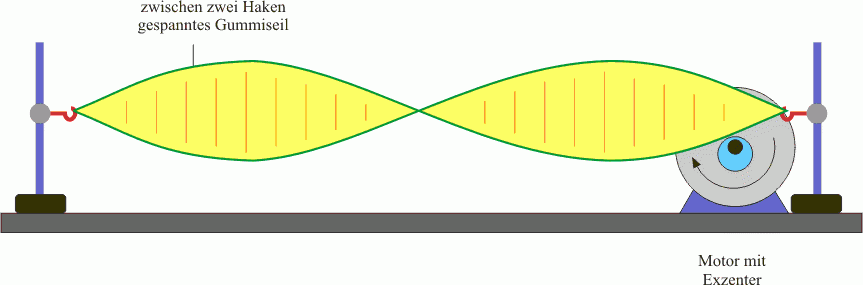
In diesem Fall kommt es nur bei ganz bestimmten Frequenzen und damit Wellenlängen der Schallwelle zur Ausbildung einer ausgeprägten stehenden Welle. Eine ähnliche Beobachtung lässt sich auch bei Querwellen z.B. bei einem Gummiseil, das auf der linken Seite fest eingespannt ist und auf der rechten Seite durch einen Excenter angeregt wird, beobachten.

Da Querwellen bildlich leichter darzustellen sind, soll am Beispiel des Gummiseiles geklärt werden, warum sich ausgeprägte stehende Wellen (die man dann auch Eigenschwingungen nennt) nur bei bestimmten Frequenzen (die man dann als Eigenfrequenzen bezeichnet) bzw. Wellenlängen der ursprünglich fortscheitenden Welle auftreten.

Hinweis: Bei den Animationen wurde der Einfachheit halber angenommen, dass die reflektierten Wellen alle die gleichen Amplituden besitzen. Außerdem wurden nur die ersten Reflexionen angedeutet. Hinlaufende- und rücklaufende Welle durchdringen sich, da dies zeichnerisch unübersichtlich würde, haben wir die Reflexionen in mehreren Bildern untereinander dargestellt.

Zusammenfassung

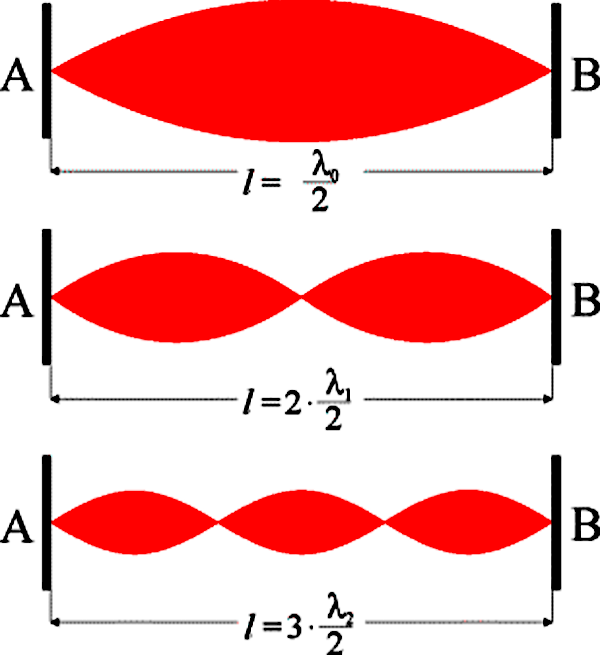
Bei bestimmten Anregungsfrequenzen bilden sich ausgeprägte Schwingungszustände aus:

Grundschwingung: \[l = \frac{{{\lambda _0}}}{2} \Leftrightarrow {\lambda _0} = 2 \cdot l\] \[{f_0} = \frac{c}{{{\lambda _0}}} = \frac{c}{{2 \cdot l}}\]
1. Oberschwingung: \[l = 2 \cdot \frac{{{\lambda _1}}}{2} \Leftrightarrow {\lambda _1} = l\] \[{f_1} = \frac{c}{{{\lambda _1}}} = \frac{c}{l}\]
2. Oberschwingung: \[l = 3 \cdot \frac{{{\lambda _2}}}{2} \Leftrightarrow {\lambda _2} = \frac{2}{3} \cdot l\] \[{f_2} = \frac{c}{{{\lambda _2}}} = 3 \cdot \frac{c}{{2 \cdot l}}\]
usw.	usw.

Erklärung:

Es kommt zu konstruktiver Überlagerung, wenn die Welle nach der Reflexion an A und an B (Hin- und Rücklauf) mit der vom Excenter neu angeregten Welle in Phase ist.

Hinweise:

• Betrachte auch die Experimente zu stehenden Quer- und Längswellen an Federn und Seilen.
• Stehende Schallwellen treten auch beim Versuch nach Kundt und durch Anregung mit einer Stimmgabel im Glasrohr auf.