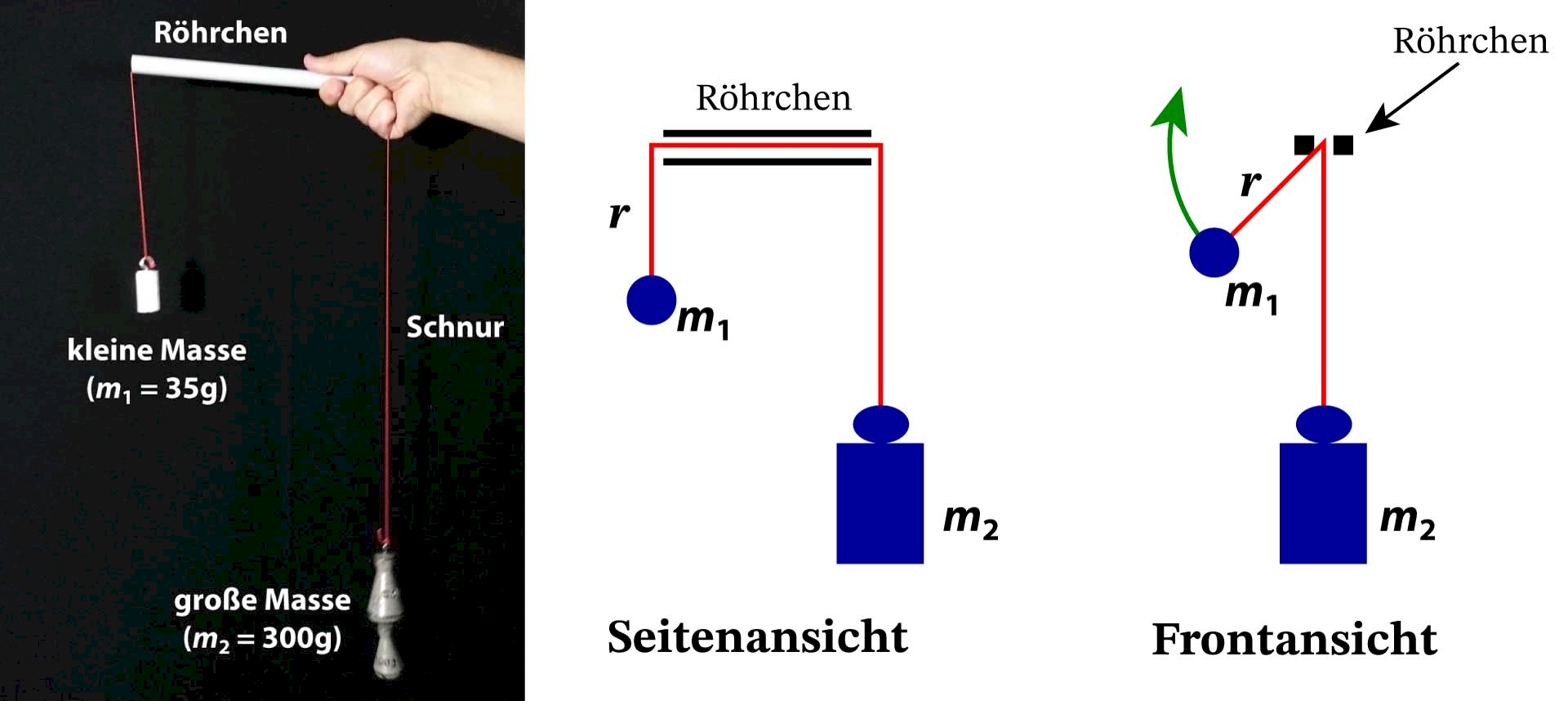
Material und Versuchsaufbau
Für den Versuch benötigst du zwei unterschiedlich große Massestücke, die mit einer glatten Schnur verbunden werden. Dazu noch ein Plastikröhrchen, durch durch das die Schnur läuft. Im Folgenden werden eine kleine Masse mit \(m_1=35\,\rm{g}\), eine große Masse mit \(m_2=300\,\rm{g}\), und eine Maurerschnur aus Polyamid genutzt.
Versuchsdurchführung mit horizontaler Kreisbahn
Der Versuch kann in unterschiedlichen Varianten und mit unterschiedlichen inhaltlichen Schwerpunkten durchgeführt werden. So kannst du das Röhrchen so halten und bewegen, dass die kleine Masse eine Kreisbahn in horizontaler Ebene durchführt. Dies kann gut als Modell für die Kurvenfahrt eines Autos genutzt werden. Entsprechend liegt der Fokus hier auf dem Zusammenhang von Bahngeschwindigkeit \(v\) der Masse \(m_1\) und dem Radius \(r\) der Kreisbahn bzw. der Höhe der Masse \(m_2\).
Achtung: Unbedingt Sicherheitsvorschriften beachten und rotierende Masse gegen Wegfliegen sichern!
Beobachtung:
Ein Steigen der Bahngeschwindigkeit \(v\) führt zu einer Zunahme des Bahnradius \(r\). Dies wird auch durch die zunehmende Höhe der Masse \(m_2\) sichtbar.
Erklärung:
Die Zentripetalkraft hat einen konstanten Betrag \(F_{\rm{ZP}}\), der durch die Gewichtskraft des Massestücks \(m_2\) und die Reibungskraft vorgegeben ist. Der Einfluss der Gewichtskraft von \(m_1\) kann vernachlässigt werden. Eine steigende Bahngeschwindigkeit \(v\) kann daher nach \(F_{\rm{ZP}}=m_1\frac{v^2}{r}\) nur durch einen größeren Radius ausgeglichen werden.
Übertragen auf den Fall des Autos bei der Kurvenfahrt, bei dem die maximale Haftkraft zwischen Autoreifen und Straßenbelag konstant ist, bedeutet dies: Eine höhere Fahrzeuggeschwindigkeit führt zu einem größeren Kurvenradius. Da dieser jedoch in der Regel vom Straßenverlauf vorgegeben ist, musst du deine Geschwindigkeit entsprechend anpassen.
Versuchsdurchführung mit vertikaler Kreisbahn
Du kannst das Plastikröhrchen aber auch so bewegen, dass die kleine Masse eine Kreisbahn in vertikaler Ebene macht. Der Fokus kann dabei auch auf den Zusammenhängen zwischen der Winkelgeschwindigkeit \(\omega\), dem Radius \(r\) der Kreisbahn und der Höhe der großen Masse \(m_2\) liegen. Dabei lässt die Winkelgeschwindigkeit \(\omega\) qualitativ besonders gut über die Umlaufdauer \(T\) beobachten. Ergänzend zur Kurvenfahrt eines Autos kann dabei auch Bezug auf die feste Bahn eines Satelliten um die Erde genommen werden.
Beobachtung
Es besteht ein Zusammenhang zwischen dem Radius der Kreisbahn und damit der Höhe des großen Massestücks und der Winkelgeschwindigkeit \(\omega\) bei stabilen Kreisbahnen:
- Ist der Radius \(r\) klein (und die Höhe des Massestücks gering), so muss die Winkelgeschwindigkeit \(\omega\) groß sein.
- Ist der Radius \(r\) groß (und damit die Höhe des Massestücks groß), so muss die Winkelgeschwindigkeit \(\omega\) gering sein.
Erklärung
Im Versuch hat die Zentripetalkraft (unter Vernachlässigung der Gewichtskraft durch das kleine Massestück) einen konstanten Betrag \({F_{{\rm{ZP}}}}\). Der Betrag ist durch die Gewichtskraft des großen Massestücks und die Reibungskraft vorgegeben. Im Falle einer statischen Kreisbahn mit konstantem Radius gilt daher \[F_{\rm{g}}={F_{{\rm{ZP}}}}=m_1\cdot r\cdot \omega ^2\] Eine höhere Winkelgeschwindigkeit \(\omega \) geht daher bei konstanter rotierender Masse \(m_1\) und konstantem Betrag der Zentripetalkraft wegen \({F_{{\rm{ZP}}}} = m_1 \cdot r \omega ^2\) mit einem kleineren Radius \(r\) der Kreisbahn einher. Ebenso muss bei einer geringeren Winkelgeschwindigkeit \(\omega\) der Radius \(r\) der Kreisbahn größer sein.
Übertragen auf einen Satelliten in einem festen Abstand von der Erdoberfläche bedeutet dies: je näher der Satellit um Erdoberfläche kreist, desto höher muss seine Winkelgeschwindigkeit sein und desto schneller umkreist er die Erde. Ist der Abstand Satellit-Erde größer, so ist die Winkelgeschwindigkeit geringer und der Satellit benötigt länger, um die Erde zu umkreisen.
Aufgabe
Berechne den Radius der stabilen Kreisbahn eines kleinen Massestücks mit \(m_1= 35{,}0\,\rm{g}\), wenn dass große Massestück eine Masse von \(m_2= 300\,\rm{g}\) besitzt und die Winkelgeschwindigkeit \(\omega= 6\cdot \pi\,\rm{s^{-1}}\) ist. Vernachlässige dabei die Gewichtskraft des kleinen Massestücks.