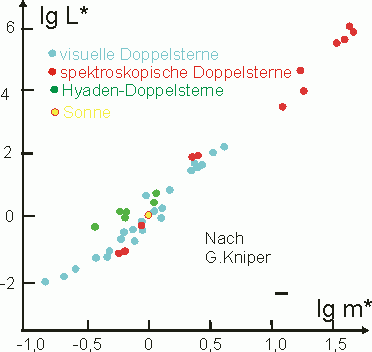Vergleicht man bei Sternen oder Doppelsternen der Hauptreihe die Leuchtkraft \(L\) bzw. die absolute Helligkeit und die Masse \(m\) so erhält man den in Abb. 1 skizzierten Zusammenhang.
Im doppelt- logarithmischen Maßstab liegen alle Hauptreihensterne in erster Näherung auf einer Geraden mit der Steigung 3. Hieraus folgt die sog. Masse-Leuchtkraft-Beziehung:\[L\sim M^3\qquad \text{bzw.}\qquad L^{*}=\left(M^{*}\right)^3\]Eine etwas genauere empirische Beziehung unterscheidet zwischen Sternmassen. So erhält man z.B.: \[L\sim M^{2,5}\qquad \text{für}\qquad M\lt 0,5 M_{\bigodot}\]\[L\sim M^{3,8}\qquad \text{für}\qquad M\gt 0,5 M_{\bigodot}\]Wobei \(M_{\bigodot}\) die Masse der Sonne beschreibt. Darüber hinaus gibt es noch feinere Einstellungen.
Mithilfe der Masse-Leuchtkraft-Beziehung kann man also nur mithilfe der beobachteten Leuchtkraft die Masse eines Sterns abschätzen.
Physikalische Erklärung:
Eine größere Masse \(M\) benötigt zur Verhinderung des Gravitationskollaps einen höheren Druck. Dieser höhere Druck bewirkt wiederum eine höhere Temperatur \(T\) des Sterns und damit eine größere Leuchtkraft \(L\). Daraus folgt, dass die Hauptreihensterne im Hertzsprung-Russel-Diagramm der Masse nach aufsteigend von rechts unten nach links oben geordnet sind.
Aufgabe
Berechne die Leuchtkraft und die absolute Helligkeit eines Hauptreihensterns der zehnfachen Sonnenmasse.