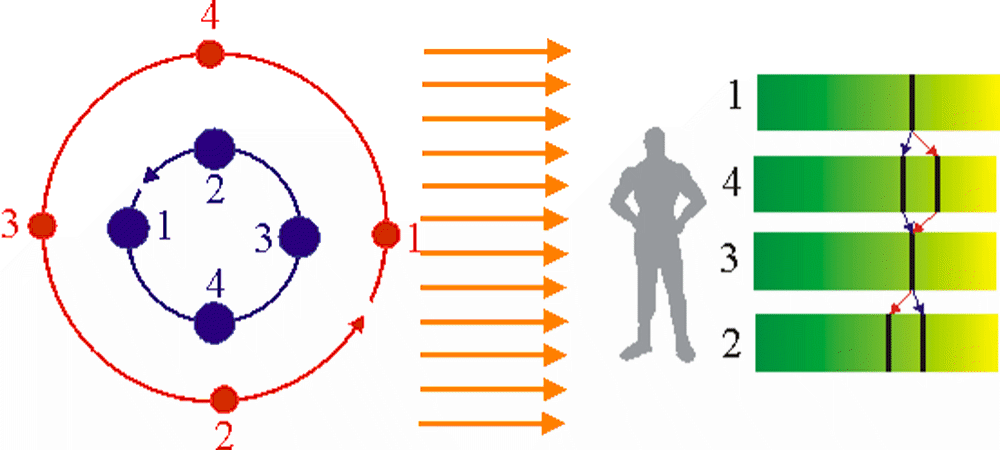
Abb. 1 Beobachtet man einen Doppelstern aus einem Punkt der gemeinsamen Bahnebene der beiden Sterne, so bewegen sich die beiden Sterne im Gegenrythmus auf uns zu bzw. von uns weg.
Beobachtet man einen Doppelstern aus einem Punkt der gemeinsamen Bahnebene der beiden Sterne, so bewegen sich die beiden Sterne im Gegenrythmus auf uns zu bzw. von uns weg.
Bei dieser Bewegung verschieben sich die charakteristischen Absorptionslinien beider Sterne im Gegenrythmus und man kann die radialen Geschwindigkeitskomponenten beider Sterne bestimmen, selbst wenn man die beiden Sterne nicht getrennt sehen kann, weil das Auflösungsvermögen des Teleskops nicht ausreicht.
Die Radialkomponente ergibt sich aus dem Dopplereffekt durch\[{v_R} = \frac{{\Delta \lambda }}{\lambda } \cdot c\]Die Umlaufdauer \(T\) bestimmt man aus den Zeitabständen zugehöriger Dopplerverschiebungen: z.B: \(0{,}5 \cdot T = t_3-t_1\)
Für den Fall von Kreisbahnen findet man:
Wegen \(v = \frac{{2r\pi }}{T}\) gilt: \(\frac{{{v_B}}}{{{v_A}}} = \frac{{{r_B}}}{{{r_A}}}\)
Wegen des Schwerpunktsatzes gilt:
mA·rA = mB·rB =>\(\frac{{{m_A}}}{{{m_B}}} = \frac{{{r_B}}}{{{r_A}}}\)
Man kann aus \(v = \frac{{2r\pi }}{T}\) bei bekanntem v und bekanntem T für jede Komponente den Radius bestimmen:
\({r_A} = \frac{{{v_A} \cdot T}}{{2\pi }}\) ;\({r_B} = \frac{{{v_B} \cdot T}}{{2\pi }}\) ; \({r_A} + {r_B} = \frac{{({v_A} + {v_B}) \cdot T}}{{2\pi }}\)
Ist der Beobachter außerhalb der Bahnebene, so erhält man über die Dopplerverschiebung nur die Projektion der Bahngeschwindigkeit auf die Beobachtungsrichtung: Über den Winkel \(\varphi\) der Bahnebene zur Projektionsrichtung kann man aber die Geschwindigkeiten berechnen. \(v_{\rm{Proj}} = v \cdot sin \, \varphi\).
Aufgabe
Aufgabe
Der helle Stern Spica im Sternbild Jungfrau ist ein spektroskopischer Doppelstern mit einer sehr kurzen Periode von genau \(4,0\) Tagen. Die Hα -Linie mit der Wellenlänge von \( {\lambda}_0 = 656,5 nm\) wird jeweils um \( \Delta {\lambda}_1 = 0,25 nm\) bzw. \(\Delta {\lambda}_2 = 0,42 nm\) gegenläufig verschoben, sofern sich der Beobachter in der Bahnebene befindet. Berechnen Sie die Geschwindigkeiten, Bahnradien sowie Massen der beiden Komponenten von Spica.