Bestimmung der Lichtenergie E im Laserblitz:
\[E = P \cdot \Delta t \Rightarrow E = 1,0 \cdot {10^8} \cdot 1,0 \cdot {10^{ - 8}}W \cdot s = 1,0\,J\]
Bestimmung der Photonenenergie Eph:
\[{E_{ph}} = \frac{{h \cdot c}}{\lambda } \Rightarrow {E_{ph}} = \frac{{6,63 \cdot 1{0^{ - 34}} \cdot 3,00 \cdot 1{0^8}}}{{693 \cdot {{10}^{ - 9}}}}\frac{{J \cdot s \cdot {\textstyle{m \over s}}}}{m} \approx 2,9 \cdot {10^{ - 19}}J\]
Berechnung der Photonenzahl Nph im Laserblitz:
\[{N_{ph}} = \frac{E}{{{E_{ph}}}} \Rightarrow {N_{ph}} = \frac{{1,0}}{{2,9 \cdot {{10}^{ - 19}}}}\frac{J}{J} \approx 3,5 \cdot {10^{18}}\]
Impulsänderung Δpph eines Photons (totale Reflexion):
\[\Delta {p_{ph}} = 2 \cdot {p_{ph}} \Rightarrow \Delta {p_{ph}} = 2 \cdot \frac{h}{\lambda } \Rightarrow \Delta {p_{ph}} = 2 \cdot \frac{{6,63 \cdot {{10}^{ - 34}}}}{{693 \cdot {{10}^{ - 9}}}}\frac{{J \cdot s}}{m} \approx 1,9 \cdot {10^{ - 27}}Ns\]
Gesamte Impulsänderung Δp aller Photonen:
\[\Delta p = {N_{ph}} \cdot \Delta {p_{ph}} \Rightarrow \Delta p = \cdot 3,5 \cdot {10^{18}} \cdot 1,9 \cdot {10^{ - 27}}Ns \approx 6,7 \cdot {10^{ - 9}}Ns\]
Nach dem Impulserhaltungssatz muss die gesamte Impulsänderung Δp aller Photonen gleich der Impulsänderung des Spiegels Δpsp sein. Da der Spiegel vor der Wechselwirkung in Ruhe war, gilt für den Betrag der Geschwindigkeit v0, mit der sich der Spiegel in Bewegung setzt:
\[\Delta {p_{sp}} = m \cdot {v_0} - 0 \Rightarrow {v_0} = \frac{{\Delta {p_{sp}}}}{m} \Rightarrow {v_0} = \frac{{6,7 \cdot {{10}^{ - 9}}}}{{2,0 \cdot {{10}^{ - 5}}}}\frac{{N \cdot s}}{{kg}} \approx 3,3 \cdot {10^{ - 4}}\frac{m}{s}\]
Zu Beginn der Spiegelbewegung liegt nur kinetische Energie vor. Diese kinetische Energie wird in Lageenergie umgesetzt. Aus dem Energiesatz folgt, dass die Lageenergie im höchsten Punkt der Spiegelauslenkung gleich der kinetischen Energie des Spiegels am Anfang der Bewegung ist:
\[m \cdot g \cdot d = \frac{1}{2} \cdot m \cdot v_0^2 \Rightarrow d = \frac{{v_0^2}}{{2 \cdot g}} \Rightarrow d = \frac{{{{\left( {3,3 \cdot {{10}^{ - 4}}} \right)}^2}}}{{2 \cdot 9,81}}m \approx 5,7 \cdot {10^{ - 9}}m\]
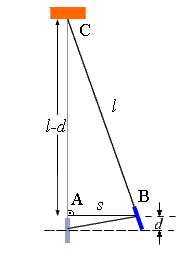
Berechnung der Strecke s aus l und d: Im Dreieck ABD gilt nach Pythagoras:
\[{l^2} = {\left( {l - d} \right)^2} + {s^2} \Rightarrow {l^2} = {l^2} - 2 \cdot l \cdot d + {d^2} + {s^2}\]
Für \({d\; \ll l}\) ergibt sich dann
\[\begin{array}{l}2 \cdot l \cdot d \approx {s^2} \Rightarrow s \approx \sqrt {2 \cdot l \cdot d} \\s \approx \sqrt {2 \cdot 0,10 \cdot 5,7 \cdot 1{0^{ - 9}}} m \approx 3,4 \cdot {10^{ - 5}}m\end{array}\]

