Arbeit im homogenen Bereich des Gravitationsfeldes
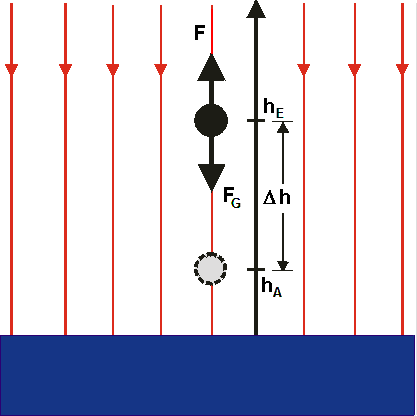
Sie haben ja bereits Erfahrung mit der Arbeitsberechnung im Gravitationsfeld; für die Hubarbeit im homogenen Bereich des Gravitationsfeldes gilt nämlich bekanntlich
\[\Delta {W_{{\rm{Hub}}}} = F \cdot \Delta h = m \cdot g \cdot \Delta h\]
Dieser Berechnung liegt zu Grunde, dass sich der Betrag der Gravitationskraft längs des Weges nicht ändert, was im homogenen Bereich gegeben ist. Wird die Änderung der Höhe \(\Delta h\) jedoch sehr groß, so ist dies nicht mehr erfüllt, da das Gravitationsfeld mit zunehmendem Abstand schwächer wird.
Berücksichtigung des Gravitationsgesetzes
Wie hat man aber vorzugehen, wenn die Ortsveränderung im Gravitationsfeld so groß ist, dass diese vereinfachende Annahme nicht mehr zulässig ist und man vom Gravitationsgesetz
\[{F_{\rm{G}}} = G \cdot \frac{{m \cdot M}}{{{r^2}}}\]
ausgehen muss?
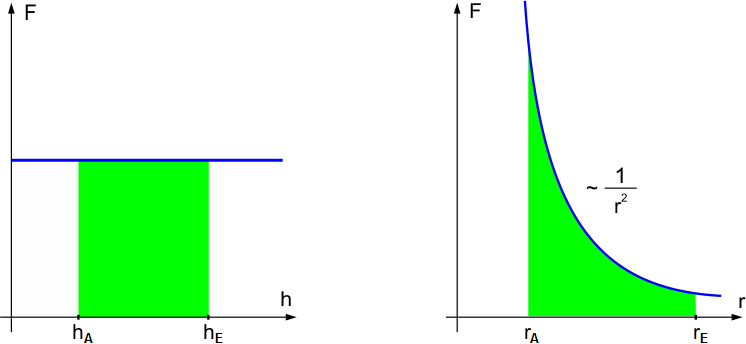
Man kommt der Lösung nahe, wenn man sich an die grafische Interpretation der Arbeitsberechnung erinnert: Die Arbeit wird im Arbeitsdiagramm dargestellt als der Flächeninhalt von Flächen unter \(s\)-\(F\)- bzw. \(h\)-\(F\)- bzw. \(r\)-\(F\)-Graphen.
Fläche unter dem Graphen entspricht der Arbeit
Die Arbeitsberechnung im Gravitationsfeld erfordert die Berechnung des Flächeninhalts unter einem nicht geradlinigen Graphen. Dies leistet i.A. die Integralrechnung, die Sie später in der Mathematik erlernen werden. Bei unserem speziellen Problem, der Berechnung des Flächeninhalts unter dem \(\frac{1}{{{r^2}}}\)-Graphen, kommen wir auch ohne Integralrechnung aus, wenn wir geschickt vorgehen.
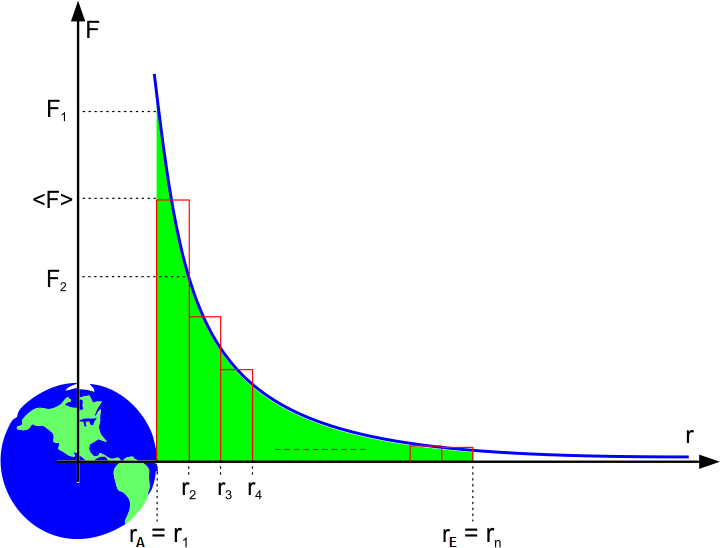
Zunächst nähern wir die Fläche unter dem \(\frac{1}{{{r^2}}}\)-Graphen durch kleine Rechtecke an (die Annäherung wird besonders gut, wenn wir viele schmale Rechtecke verwenden). Für die Höhe dieser Rechtecke wählen wir einen Mittelwert \(\left\langle F \right\rangle \), der zwischen der maximalen Kraft am linken und der minimalen Kraft am rechten Rand des betrachteten Intervalls liegt. Für den Arbeitsbetrag \(\Delta W_1\), der dem ersten (linken) Rechteck zugeordnet ist, gilt
\[\Delta {W_{\rm{1}}} = \left\langle F \right\rangle \cdot \left( {{r_2} - {r_1}} \right) \quad(1)\]
Eine brauchbare Näherung für \(\left\langle F \right\rangle \) ist das geometrische Mittel aus \(F_1\) und \(F_2\):
\[\begin{eqnarray}\left\langle F \right\rangle &=& \sqrt {{F_1} \cdot {F_2}} \\ &=& \sqrt {G \cdot \frac{{m \cdot M}}{{{r_1}^2}} \cdot G \cdot \frac{{m \cdot M}}{{{r_2}^2}}} \\ &=& G \cdot \frac{{m \cdot M}}{{{r_1} \cdot {r_2}}} \quad(2)\end{eqnarray}\]
Setzt man \((2)\) in \((1)\) ein, so erhält man
\[\Delta {W_{\rm{1}}} = G \cdot \frac{{m \cdot M}}{{{r_1} \cdot {r_2}}} \cdot \left( {{r_2} - {r_1}} \right) = G \cdot m \cdot M \cdot \left( {\frac{{{r_2}}}{{{r_1} \cdot {r_2}}} - \frac{{{r_1}}}{{{r_1} \cdot {r_2}}}} \right) = G \cdot m \cdot M \cdot \left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)\]
Man erhält die gesamte Arbeit \(\Delta {W_{{\rm{ges}}}}\), indem man alle Teilarbeiten aufaddiert:
\[\begin{eqnarray}\Delta {W_{{\rm{ges}}}} &=& \Delta {W_{\rm{1}}} + \Delta {W_{\rm{2}}} + \Delta {W_{\rm{3}}} + ... + \Delta {W_{{\rm{n - 1}}}}\\ &=& G \cdot m \cdot M \cdot \left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right) + G \cdot m \cdot M \cdot \left( {\frac{1}{{{r_2}}} - \frac{1}{{{r_3}}}} \right) + G \cdot m \cdot M \cdot \left( {\frac{1}{{{r_3}}} - \frac{1}{{{r_4}}}} \right) + ... + G \cdot m \cdot M \cdot \left( {\frac{1}{{{r_{n - 1}}}} - \frac{1}{{{r_n}}}} \right)\\ &=& G \cdot m \cdot M \cdot \left( {\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right) + \left( {\frac{1}{{{r_2}}} - \frac{1}{{{r_3}}}} \right) + \left( {\frac{1}{{{r_3}}} - \frac{1}{{{r_4}}}} \right) + ... + \left( {\frac{1}{{{r_{n - 1}}}} - \frac{1}{{{r_n}}}} \right)} \right)\\ &=& G \cdot m \cdot M \cdot \left( {\frac{1}{{{r_1}}}\underbrace { - \frac{1}{{{r_2}}} + \frac{1}{{{r_2}}}}_{ = 0}\underbrace { - \frac{1}{{{r_3}}} + \frac{1}{{{r_3}}}}_{ = 0}\underbrace { - \frac{1}{{{r_4}}} + ... + \frac{1}{{{r_{n - 1}}}}}_{ = 0} - \frac{1}{{{r_n}}}} \right)\\ &=& G \cdot m \cdot M \cdot \left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_n}}}} \right)\\ &=& G \cdot m \cdot M \cdot \left( {\frac{1}{{{r_{\rm{A}}}}} - \frac{1}{{{r_{\rm{E}}}}}} \right)\end{eqnarray}\]
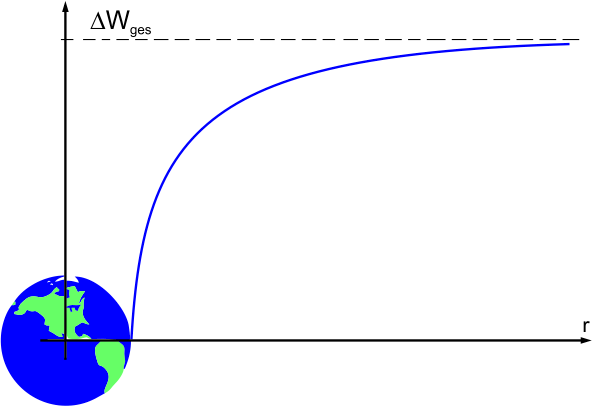
Graphische Darstellung der notwendigen Arbeit
Die Abbildung rechts zeigt nun die Gesamtarbeit \(\Delta {W_{{\rm{ges}}}}\), die man benötigt, um einen Körper von der Erdoberfläche \(r_{\rm{A}}\) bis hin zu einer Entfernung \(r\) vom Erdmittelpunkt zu bewegen. Man sieht an dem Graphen, dass die Arbeit mit wachsendem \(r\) in unmittelbarer Nähe der Erdoberfläche stark zunimmt. Je weiter man sich jedoch von der Erde entfernt, desto geringer ist die Zunahme der Gesamtarbeit für eine bestimmte Strecke. Dies ist auf Grund der \(\frac{1}{{{r^2}}}\)-Abhängigkeit der Gravitationskraft auch zu vermuten.