Der Drehimpuls \(\vec L\) ist das Produkt aus dem Trägheitsmoment \(J\) und der Winkelgeschwindigkeit \(\vec \omega \). Es gilt:\[L = J \cdot \omega \]Der Vektor des Drehimpulses hat dabei die gleiche Richtung wie die Winkelgeschwindigkeit \(\omega\).
Drehimpulserhaltung
Analog zum Impulserhaltungssatz existiert auch ein Drehimpulserhaltungssatz. Dieser lautet: In einem abgeschlossenen System bleibt der Gesamtdrehimpuls konstant, wenn kein äußeres Drehmoment wirkt.
Drehimpuls und Drehimpulserhaltung
Der Drehimpuls \(\vec{L}\) eines Körpers ist \[\vec{L}=J\cdot\vec{\omega}\]wobei \(J\) sein Trägheitsmoment und \(\vec{\omega}\) seine Winkelgeschwindigkeit ist. Da der Drehimpulsvektor die gleiche Richtung wie die Winkelgeschwindigkeit besitzt, kannst du auch mit Skalaren, also \(L=J\cdot\omega\), rechnen.
Der Drehimpuls ist eine Erhaltungsgröße. In einem abgeschlossenen System bleibt der Gesamtdrehimpuls konstant, wenn kein äußeres Drehmoment wirkt.
Folgen des Drehimpulserhaltungssatzes
Aus der Drehimpulserhaltung ergeben sich verschiedenste Phänomene: Der Eiskunstläufer, der bei der Pirouette moderat dreht, wenn er die Arme und Beine weit nach außen gibt, dreht sich schneller, wenn er Arme und Beine anzieht, also nahe zur Drehachse bringt (vgl. Abb. 1).
Der Grund dafür ist folgender: Sind die Massen der Arme und Beine weit von der Drehachse, dann ist sein Trägheitsmoment \(J\) groß. Bringt er die Massen von Armen und Beinen näher zur Drehachse, so verringert sich sein Trägheitsmoment \( J\). Da das Produkt aus Trägheitsmoment und Winkelgeschwindigkeit aber gleich bleiben muss, erhöht sich entsprechend die Winkelgeschwindigkeit \(\omega \), wenn sich das Trägheitsmoment \(J\) verkleinert.
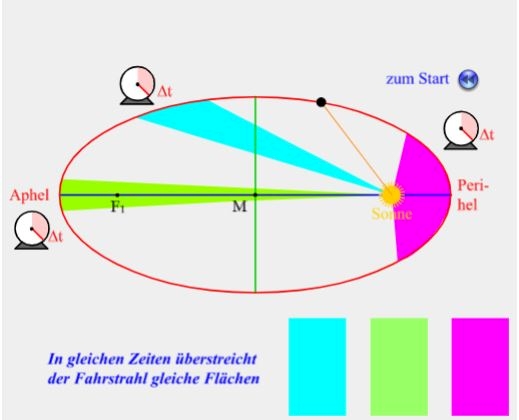
Der Planet, der sich auf einer Ellipsenbahn um die Sonne bewegt ist umso schneller, je näher er der Sonne ist. Diese Konsequenz des Drehimpulserhaltungssatzes hat Johannes KEPLER bereits herausgefunden. Er formulierte das 2. KEPLER-Gesetz: Der Fahrstrahl eines Planeten überstreicht in gleichen Zeiten gleiche Flächen (vgl. Abb. 2).