Energie in rotierendem System
Dreht sich ein Rad mit konstanter Winkelgeschwindigkeit \(\omega \) um eine feste Drehachse, so bewegen sich jeweils gegenüberliegende Punkte mit entgegengesetzter Geschwindigkeit. Der Massenschwerpunkt bewegt sich also nicht und das Rad besitzt keine Bewegungsenergie als Ganzes. Trotzdem steckt in ihm Energie, die man als Rotationsenergie \({E_\rm{Rot}}\) bezeichnet. Diese Energie ist aber nichts anderes als die Summe der kinetischen Energien der einzelnen Massenpunkte des Rades. Heben sich die Impulse der einzelnen Massenpunkte bei der Drehbewegung wegen der Gegenläufigkeit auf, so tun die kinetischen Energien dies nicht, da kinetische Energien im Gegensatz zu Impulsen und Geschwindigkeiten keine Richtung haben und sich deshalb die Beträge aufsummieren anstatt zu subtrahieren.
Berechnung der Rotationsenergie
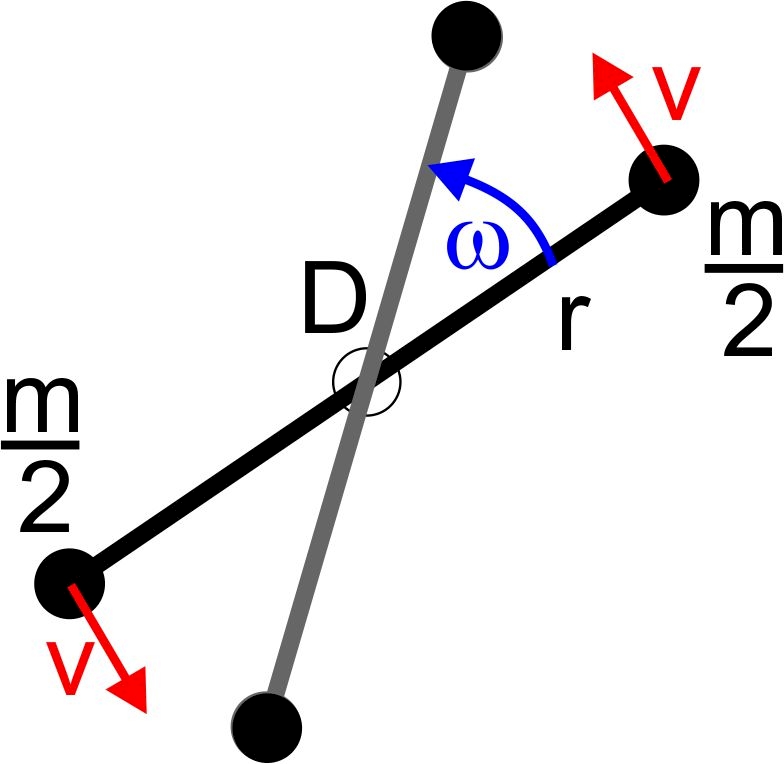
Wie groß die Rotationsenergie ist, lässt sich am einfachsten an einer sich mit der Winkelgeschwindigkeit \(\omega \) um eine Drehachse D drehende symmetrische Hantel zeigen, wie sie in Abb. 2 zu sehen ist. Denken wir uns die Gesamtmasse \(m\) auf zwei Hälften verteilt, so gilt für die kinetische Energie jeder dieser Hälften\[{E_\rm{kin}} = \frac{1}{2} \cdot \frac{m}{2} \cdot {v^2}\]Da die Geschwindigkeit das Produkt aus Radius und Winkelgeschwindigkeit ist (\(v = r \cdot \omega \)) und die Rotationsenergie die Summe der kinetischen Energien der beiden Hantelhälften ist, gilt\[{E_\rm{Rot}} = 2 \cdot \frac{1}{2} \cdot \frac{m}{2} \cdot {\left( {r \cdot \omega } \right)^2} = \frac{1}{2} \cdot m \cdot {r^2} \cdot {\omega ^2}\]
Daraus ergibt sich für die Rotationsenergie\[{E_\rm{Rot}} = \frac{1}{2} \cdot J \cdot {\omega ^2}\]wobei \(J\) das sogenannte Trägheitsmoment ist.
Trägheitsmoment
Für besondere Fälle, in denen das rotierende System eine gewisse Symmetrie aufweist, lässt sich das Trägheitsmoment \(J\) relativ einfach berechnen. So ist das Trägheitsmoment für eine Hantel oder ein Rad, bei dem alle Massepunkte den gleichen Abstand \(r\) von der Drehachse haben\[{J_\rm{Hantel}} = m \cdot {r^2}\]Das Trägheitsmoment einer um seine Symmetrieachse sich drehenden homogenen Scheibe bzw. Zylinder beträgt\[{J_\rm{Zylinder}} = \frac{1}{2} \cdot m \cdot {r^2}\]Das Trägheitsmoment einer homogenen Kugel, deren Achse durch den Mittelpunkt geht beträgt\[{J_\rm{Kugel}} = \frac{2}{5} \cdot m \cdot {r^2}\]Für Körper, bei denen die Massepunkte unterschiedliche Abstände von der Drehachse haben, berechnet sich das Trägheitsmoment durch Aufsummierung (bzw. Integration) aller Einzelträgheitsmomente.\[J = \int {{r^2}d} m\]Allgemein ist das Trägheitsmoment eines Körpers eine von seiner Rotationsachse abhängige skalare Größe.