Versuchsaufbau
Abb. 1 zeigt dir die Schaltskizze des Aufbaus, mit dem im Versuch eine ungedämpfte elektromagnetische Schwingung demonstriert werden könnte, wenn die Bauteile keinen OHMschen Widerstand hätten. Dazu werden folgende Bauteile genutzt:
- Eine elektrische Quelle mit der gut geglätteten Nennspannung \(U_0\) zum Aufladen des Kondensators bei Versuchsbeginn.
- Einen Umschalter \(\rm{S}\), mit dem zwischen den zwei Stromkreisen gewechselt werden kann.
- Einen Kondensator der Kapazität \(C\).
- Eine Spule der Induktivität \(L\).
- Einen Strommesser für die Stromstärke \(I\).
- Zwei Spannungsmesser für die Spannungen \(U_C\) und \(U_L\).
- Optional: ein dritter Spannungsmesser für die Spannung \(U_0\).
- Optional: Ein Widerstand, der den Ladestrom des Kondensators begrenzt.
Einsatz eines Messwerterfassungssystems
Für quantitative Untersuchungen sollte die Strom- und Spannungsmessung mit Hilfe eines Messwerterfassungssystems erfolgen. Alternativ ist auch der Einsatz eines Oszilloskops oder eines \(x\)-\(y\)-Schreibers möglich.
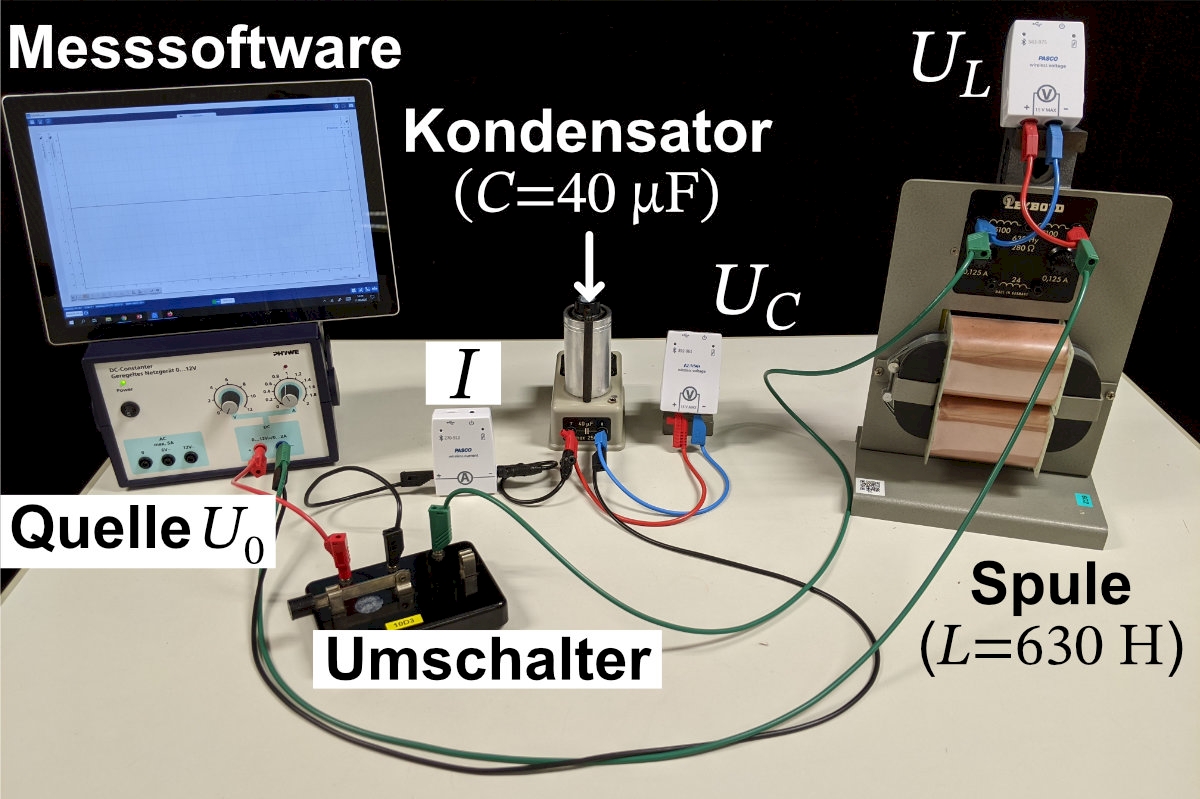
Mit kabellosen Sensoren zur Messung der Stromstärke im Schwingkreis, der Spannung \(U_C\) über dem Kondensator und der Spannung \(U_L\) über der Spule ergibt sich ein Aufbau wie in Abb. 2. Hierbei sind die Sensoren via Bluetooth mit der Messsoftware verbunden.
Hinweis: Die Polung der Messgeräte ist dabei so gewählt, dass die sich ergebenden Messwerte mit den rechnerischen Lösungen der entsprechenden Differentialgleichung übereinstimmen (siehe Grundwissen).
Mit der Messsoftware werden die Stromstärke \(I\) im \(L\,C\)-Kreis, die Spannung \(U_C\) über dem Kondensator und die Spannung \(U_L\) über der Spule aufgezeichnet. Dabei sollte die Rate der Datenerfassung bei \(100\,\rm{Hz}\) oder mehr liegen. Auch sollten alle Sensoren beim Versuchsbeginn automatisch auf Null gesetzt werden.
Versuchsdurchführung
Nach dem Starten der Messung wird zunächst der Kondensator mittels der Quelle geladen. Beachte dabei die maximal zulässige Spannung von Kondensator und Spannungssensor! Anschließend wird der Umschalter umgelegt.
Versuchsbeobachtung
In der Messwerterfassungssoftware können gegen die Zeit die drei Messwerte sowohl getrennt als auch gemeinsam in einem einzigen Diagramm dargestellt werden (vgl. Abbildung). In den Abbildungen markiert die senkrechte, rote Linie jeweils den Zeitpunkt, an dem der Schalter umgelegt wurde.
Versuchsauswertung
Die Messwerte zeigen anschaulich, dass die Spannung über dem Kondensator \(U_C\) und die Spannung über der Spule \(U_L\) jeweils genau das entgegengesetzte Vorzeichen besitzen, betragsmäßig jedoch gleich sind.
Auch lässt sich mit \(\omega=\sqrt{\frac{1}{L\cdot C}}\) die Schwingungsdauer von\[T=\frac{2\pi}{\omega}=2\cdot\pi\cdot\sqrt{L\cdot C}\]bestätigen. Mit dem genutzten Kondensator der Kapazität \(C=40\,\mu\rm{F}\) und der Spule der Induktivität von \(L=630\,\rm{H}\) ergibt sich \[T=2\cdot\pi\cdot\sqrt{630\,\rm{H}\cdot 40\,\mu\rm{F}}=1\,\rm{s}\]Dies entspricht in etwa der im Versuch gemessenen Periodendauer.
Anders als an einem idealen ungedämpften Schwingkreis zeigt sich im Experiment ein Abfall der Spannung mit der Zeit. Dieser wird maßgeblich durch den Ohmschen Widerstand der Bauteile, insbesondere der Spule mit \(R=280\,\Omega\) verursacht.
Einfluss der Kapazität \(C\) des Kondensators
Ergänzend kann mit dem Versuchsaufbau gut der Einfluss der Kapazität \(C\) des Kondensators auf die Periodendauer \(T\) der Schwingung verdeutlicht werden. Dazu ist im Versuchsaufbau der Kondensator durch verschiedene weitere Kondensatoren zu ersetzen und der Versuch erneut durchzuführen.
Aufgabe
Aufgabe
Gib an, wie die Kapazität \(C\) des Kondensators und die Induktivität \(L\) der Spule die Schwingungsdauer \(T\) eines ungedämpften Schwingkreises beeinflussen.