Wiederholung aus der Mittelstufe
Für die Hubarbeit im Labor gilt:\[W = F_{\rm g}\cdot h\qquad\text{oder}\qquad E_{\rm{pot,oben}}-E_{\rm{pot,unten}}\] Dies ist ein Spezialfall der Gleichung \(W = F\cdot s\) also Arbeit gleich Kraft mal Weg.
Diese gilt nur unter folgenden 2 Bedingungen:
1) Die Kraft \(F\) wirkt immer in Wegrichtung
2) Die Kraft ist längs des Wegs konstant
Verallgemeinerungen für den Arbeitsbegriff
-
Ist die Kraft nicht parallel zum Weg, so multipliziert man typischerweise die Kraftkomponente in Wegrichtung mit den Weg oder die Wegkomponente in Kraftrichtung mal die Kraft.
Im Gravitationsfeld ist die Arbeit ist aber nur von Anfangs- und Endpunkt, nicht jedoch vom Weg abhängig. Daher sucht man sich den günstigsten Weg, dessen erster Teil ein Wegstück ist, bei dem Weg und Kraft parallel sind, und dessen zweiter Teil ein Wegstück ist, bei dem Weg und Kraft zueinander senkrecht stehen. So bringt nur der erste Teil einen Beitrag zur Arbeit.\[W=E_{\rm{pot,Endpunkt}}-E_{\rm{pot,Anfangspunkt}}\]
-
Ist die Kraft längs des Weges nicht konstant, so besteht die Arbeit aus einer Summe kleiner Arbeitsbeträge längs kleiner Teilstücke des Weges, längs derer die Kraft sich nicht wesentlich ändert. Die Arbeit ergibt sich daher aus dem Integral \[W = \int\limits_{{r_{\rm{Anf}}}}^{{r_{\rm{End}}}} {F \cdot dr} \]Dies führt mit der Gravitationskraft \(F_{\rm{G}}=\frac{G\cdot m\cdot M}{r^2}\) zur Arbeit im Gravitationsfeld: \[W = \int\limits_{{r_{\rm{Anf}}}}^{{r_{\rm{End}}}} {G \cdot m \cdot M \cdot \frac{1}{{{r^2}}} \cdot dr} = G \cdot m \cdot M \cdot \left[ { - \frac{1}{r}} \right]_{{r_{\rm{Anf}}}}^{{r_{\rm{End}}}}\]\[W = - G \cdot m \cdot M \cdot \frac{1}{{{r_E}}} + G \cdot m \cdot M \cdot \frac{1}{{{r_A}}}=E_{\rm{pot,Endpunkt}}-E_{\rm{pot,Anfangspunkt}}\]
Weiter gilt die Festlegung, dass ein Körper im freien Weltall keine potentielle Energie besitzt. Es ist daher \(E_{\rm{pot,}\infty}=0\).
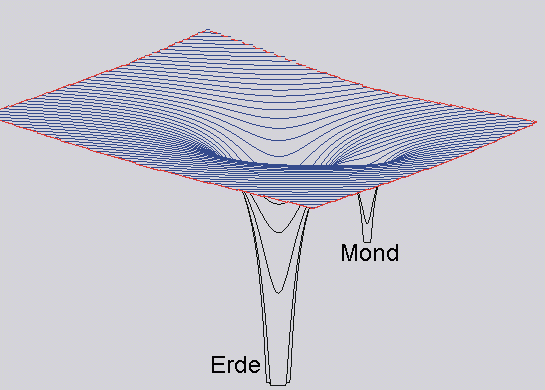
Gravitationsfeld in der Nähe von Körpern
In der Nähe eines schweren Körpers sinkt die potentielle Energie mit der Annäherung an den Körper indirekt proportional zum Abstand.
Man kann sich das Gravitationsfeld (um eine Raumdimension reduziert) in der Nähe von schweren Körpern wie in Abb. 1 skizziert vorstellen.
In der Nähe der Körper bilden sich wie in einer sich dehnenden Gummihaut auf Grund der Masse des Körpers Gruben, deren Wände mit 1/r² abfallen und längs deren Wänden andere Körper, wie Monde oder Satelliten, kreisen können, ohne den Anziehungsbereich verlassen zu können.
Berechnung der Fluchtgeschwindigkeit
Damit ein Körper das Gravitationspotential eines Planeten verlassen kann, muss dem Körper die Hubarbeit von der Körperoberfläche bis ins Unendliche in Form von kinetischer Energie mitgegeben werden:\[\frac{1}{2}m\cdot{v^2} = \frac{{G \cdot {\rm{m}} \cdot {\rm{M}}}}{r} \Rightarrow v = \sqrt {\frac{{2 \cdot G \cdot M}}{r}}\] Diese Geschwindigkeit heißt Fluchtgeschwindigkeit. Für die Erde ist die Fluchtgeschwindigkeit \(v_{\rm{Flucht}}= 11{,}2\,\rm{\frac{km}{s}}\).
Bedeutung der Fluchtgeschwindigkeit
Die Fluchtgeschwindigkeit unterscheidet sich natürlich zwischen den Himmelskörpern und hat unter anderem Einfluss auf die Atmosphäre der jeweiligen Planten. Je kleiner die Fluchtgeschwindigkeit, um so schwerer kann der Körper Gase halten bzw. um so leichter können Teilchen aus der Atmosphäre ins All entweichen. Die Bildung bzw. Beibehaltung einer Atmosphäre ist also von einer Mindestgröße der Fluchtgeschwindigkeit abhängig.