Für viele Rechnungen benötigst du astronomische Daten unseres Sonnensystems, das inzwischen schon sehr gut erforscht ist. Beachte bei den Rechenaufgaben die folgenden Punkte:
- Achte bei der Aufgabenstellung sehr genau darauf, von welchen Daten du ausgehen darfst.
- Vermeide Einheitenfehler, indem du konsequent im Meter-Kilogramm-Sekunden-System (MKS-System) arbeitest. Wandle zum Beispiel Längenangaben in \(\rm{km}\) sofort in \(\rm{m}\) um. Wandle ebenso die Umlaufdauern in Sekunden um. Dies ist zwar nicht immer der schnellste Weg, jedoch vermeidest du dadurch Fehler.
| Erde |
Masse: \({m_{\rm{E}}} = 5,977 \cdot {10^{24}}{\rm{kg}}\) Mittlerer Radius: \({R_{\rm{E}}} = 6368{\rm{km}} = 6,368 \cdot 10^6{\rm{m}}\) Mittlerer Bahnradius um die Sonne: \({r_{\rm{E}}} = 1,496 \cdot {10^8}{\rm{km}} = 1,496 \cdot {10^{11}}{\rm{m}}\) Umlaufzeit um die Sonne: \({T_{\rm{E}}} = 365,25{\rm{d}}\) Neigung der Erdachse gegenüber der Bahnebene: \(66,5^\circ \) |
|
|---|---|---|
| Sonne |
Masse: \({m_{\rm{S}}} = 1,98 \cdot {10^{30}}{\rm{kg}}\) Mittlerer Radius: \({R_{\rm{S}}} = 6,96 \cdot 10^5{\rm{km}}= 6,96 \cdot 10^8{\rm{m}}\) Fallbeschleunigung auf der Oberfläche: \({g_{\rm{S}}} = 275\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) Solarkonstante (Strahlungsleistung) auf der Erde: \(S = 1,367\frac{{{\rm{kW}}}}{{{{\rm{m}}^{\rm{2}}}}}\) |
|
| Mond |
Masse: \({m_{\rm{M}}} = 7,349 \cdot {10^{22}}{\rm{kg}}\) (\(0,0123 \cdot {m_{\rm{E}}}\)) Mittlerer Radius: \({R_{\rm{M}}} = 1738{\rm{km}} = 1,738 \cdot {\rm{1}}{{\rm{0}}^6}{\rm{m}}\) (\(0,273 \cdot {R_{\rm{E}}}\)) Mittlerer Bahnradius um die Erde: \({r_{\rm{M}}} = 384400{\rm{km}} = 3,844 \cdot {10^8}{\rm{m}}\) (\(60,3 \cdot {R_{\rm{E}}}\)) Umlaufzeit um die Erde: \({T_{\rm{M}}} = 27,1{\rm{d}}\) Fallbeschleunigung auf der Oberfläche: \({g_{\rm{M}}} = 1,63\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) |
Unser Sonnensystem besitzt 8 Planeten (und viele kleinere Planetoiden; Pluto ist seit einigen Jahren kein Planet mehr, wir führen ihn dennoch häufig noch mit auf), die um die Sonne kreisen, sowie eine große Anzahl von Monden, die um diese Planeten und Planetoiden kreisen. Jeder dieser Himmelskörper weist an seiner Oberfläche einen bestimmte Fallbeschleunigung \(g\) auf. Die Oberfläche der Planeten ist nicht immer fest. Bei gasförmigen Planeten nimmt man die äußere Gasschicht als Oberfläche an. Zur Merkregel für die Planeten verwendet man gern den Satz:
Mein Vater erklärt mir jeden Sonntag unseren Nachthimmel
oder etwas poetischer
Mächtig verliebt entzückt mich jeden Sonntag unser Nachthimmel (Dirk Hoppe)
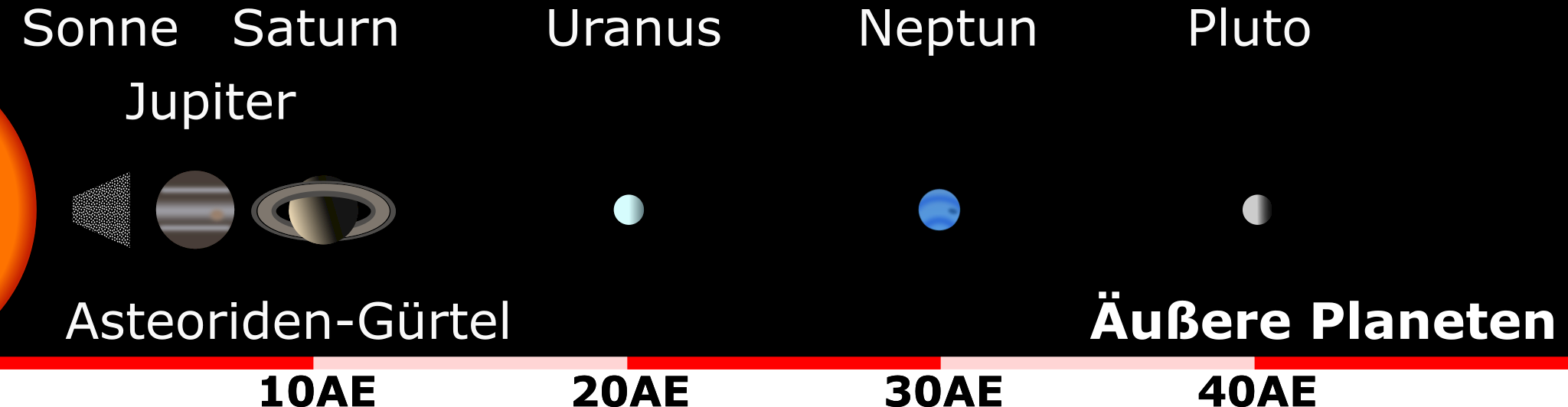
Wir unterscheiden dabei die inneren und die äußeren Planeten.
| Bahnradius (relativ zu \({r_{\rm{E}}}\)) |
Umlaufzeit | Masse (relativ zu \({m_{\rm{E}}}\)) |
Radius (relativ zu \({R_{\rm{E}}}\)) |
Fallbeschleunigung an der Oberfläche |
||
|---|---|---|---|---|---|---|
| Sonne | - | - | \(334000\) | \(109\) | \({g_{\rm{S}}} = 275\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) | |
| Merkur | \(0,387\) | \(0,241\rm{a}\) | \(0,055\) | \(0,383\) | \({g_{\rm{Me}}} = 3,70\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) | |
| Venus | \(0,723\) | \(0,615\rm{a}\) | \(0,815\) | \(0,950\) | \({g_{\rm{V}}} = 8,87\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) | |
| Erde | \(1,00\) | \(1,00\rm{a}\) | \(1,00\) | \(1,00\) | \({g_{\rm{E}}} = 9,81\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) | |
| Mars | \(1,52\) | \(1,88\rm{a}\) | \(0,107\) | \(0,533\) | \({g_{\rm{Ma}}} = 3,73\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) | |
| Jupiter | \(5,20\) | \(11,86\rm{a}\) | \(318\) | \(11,2\) | \({g_{\rm{J}}} =24,79\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) | |
| Saturn | \(9,54\) | \(29,5\rm{a}\) | \(95,2\) | \(9,41\) | \({g_{\rm{Sa}}} = 11,1\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) | |
| Uranus | \(19,2\) | \(84,0\rm{a}\) | \(14,6\) | \(4,1\) | \({g_{\rm{U}}} = 9,0\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) | |
| Neptun | \(30,1\) | \(164,8\rm{a}\) | \(17,2\) | \(3,8\) | \({g_{\rm{N}}} = 11,4\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) | |
| Pluto | \(39,8\) | \(247,7\rm{a}\) | \(0,003\) | \(0,18\) | \({g_{\rm{P}}} = 0,6\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) |