Aussehen der Exponentialfunktion
Bei einer Exponentialfunktion befindet sich die Funktionsvariable im Exponenten. Allgemein hat eine Exponentialfunktion die Form \(f(x)=a\cdot b^x+c\). Häufig ist jedoch der Parameter \(c=0\), sodass gilt \[f(x)=a\cdot b^x\] Dabei ist \(a\) der sogenannte Startwert, der auch den Schnittpunkt mit der y-Achse bestimmt. \(b\) ist der sog. Wachstumsfaktor, der maßgeblich für den weiteren Verlauf des Funktionsgraphen ist und immer eine positive Zahl sein muss.
Achtung: Die Nomenklatur ist nicht eindeutig. Häufig werden \(a\) und \(b\) auch umgekehrt genutzt. Dann ist \(f(x)=b\cdot a^x\). Hier ist dann \(b\) der Startwert und \(a\) der Wachstumsfaktor. Achte also entsprechend auf die genutzten Bezeichnungen und ihre Bedeutung.
Wachstum bei \(b>1\), Abnahme bei \(b<1\)
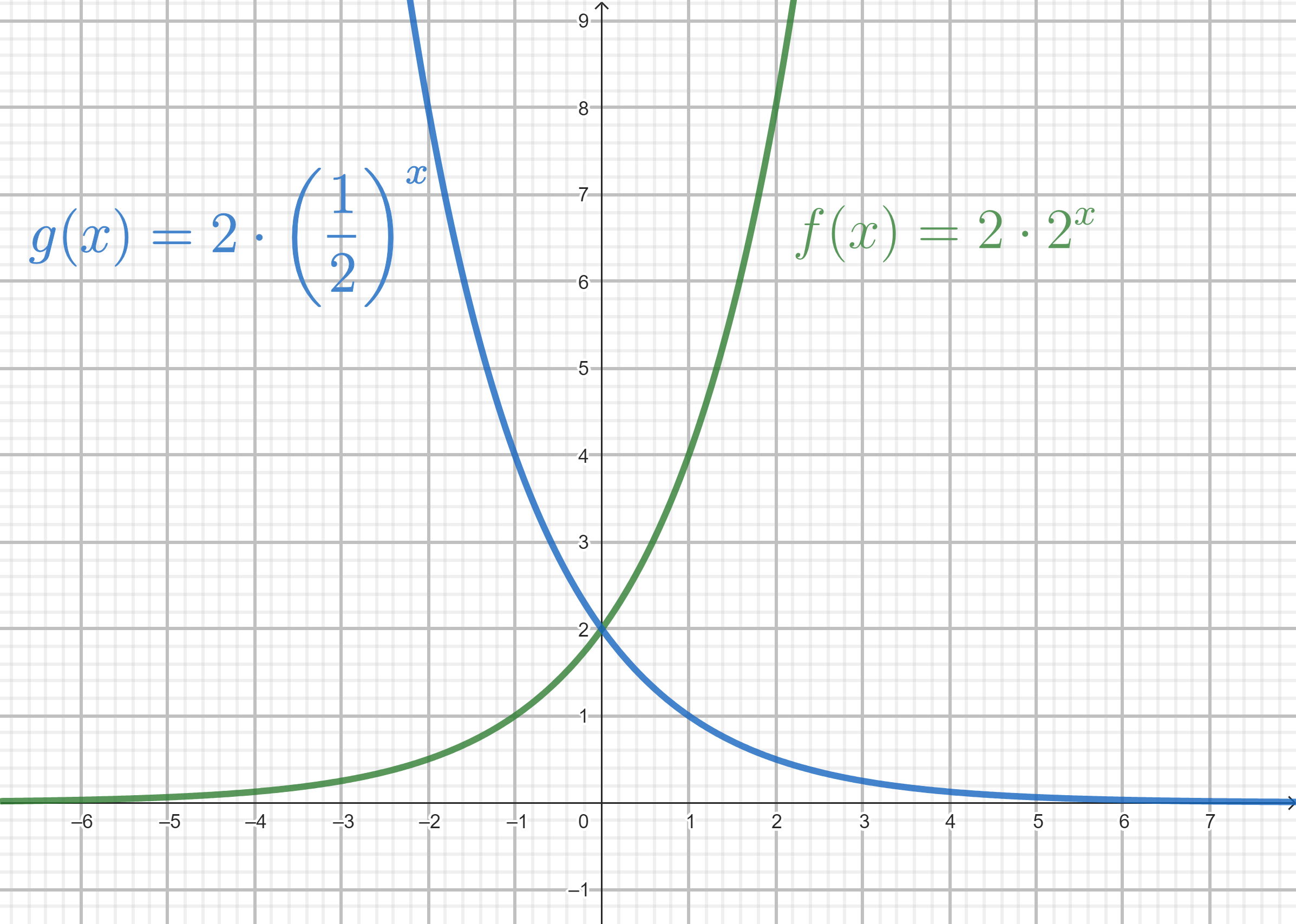
Abb. 1 zeigt den charakteristischen Verlauf einfacher Exponentialfunktionen. Ist der Wachstumsfaktor \(b\) wie bei der Funktion \(f(x)=2\cdot 2^x\) größer als 1, so wachsen die Funktionswerte mit zunehmendem \(x\). Es liegt exponentielles Wachstum vor.
Ist der Wachstumsfaktor \(b\) wie bei der Funktion \(g(x)=2\cdot \left(\frac{1}{2}\right)^x\) jedoch kleiner als 1, so nehmen die Funktionswerte mit zunehmendem \(x\) ab. Es liegt eine exponentielle Abnahme vor. Dieser Fall spielt in der Schulphysik eine wichtigere Rolle, denn mit einer solchen abnehmenden Exponentialfunktion kannst du z.B. die Entladung eines Kondensators oder den Zerfall von radioaktiven Stoffen sowie deren Aktivität beschreiben.
Darstellung mit \(e\)-Funktion
Häufig werden Exponentialfunktionen auch mittels \(e\)-Funktion dargestellt: \[f(x)=a\cdot e^{k\cdot x}\]Dabei ist \(a\) der Startwert und \(k\) beeinflusst den Verlauf maßgeblich. Für \(k>0\) liegt ein exponentielles Wachstum vor, für \(k<0\) eine exponentielle Abnahme. Die Größe \(k\) wird je nach Sachzusammenhang unterschiedlich bezeichnet, beim Zerfallsgesetz z.B. als Zerfallskonstante \(\lambda\).
Funktionsgleichung ermitteln mittles Regression
Häufig möchtest du die Funktion ermitteln, zu der gegebene oder im Experiment ermittelte Daten passen, sodass du das Verhalten allgemein beschreiben und weitere Werte berechnen kannst. Dazu zeigt Tabelle 1 beispielhafte Messwerte, die durch Messung der Aktivität eines radioaktiven Stoffes aufgenommen wurden. Der gesamte Auswerteprozess ist aber auch bei anderen exponentiellen Abnahmen wie der Entladung eines Kondensators identisch.
| \(t\;\rm{in}\;\rm{s}\) | \(1{,}0\) | \(2{,}0\) | \(3{,}0\) | \(4{,}0\) | \(5{,}0\) | \(6{,}0\) | \(7{,}0\) | \(8{,}0\) | \(9{,}0\) |
|---|---|---|---|---|---|---|---|---|---|
| \(A\;\rm{in}\;10^{6}\,\rm{Bq}\) | \(4{,}0\) | \(3{,}3\) | \(2{,}6\) | \(2{,}1\) | \(1{,}7\) | \(1{,}4\) | \(1{,}1\) | \(0{,}9\) | \(0{,}7\) |
1. Messwerte in einem Diagramm darstellen
Der erste Schritt bei der Auswertung ist meist die Darstellung der Messwerte in einem Diagramm, hier also einem Zeit-Aktivitäts- kurz \(t\)-\(A\)-Diagramm. Die Darstellung kann per Hand, in GeoGebra (vgl. Abb. 2.1), mittel GTR oder in einem Tabellenkalkulationsprogramm erfolgen.
2. Ausschluss anderer Zusammenhänge
Im Diagramm kannst du auch gut erkennen, dass es sich hier weder um einen direkt proportionalen noch um einen quadratischen Zusammenhang handelt, da der Graph keine Gerade und keinen Parabelast darstellt. Ein umgekehrt proportionaler Zusammenhang liebt ebenfalls nicht vor, da die Produktgleichheit nicht erfüllt ist und auch dem Wert Null auf der Rechtsachse ein sinnvoller Wert auf der Hochachse zugeordnet werden kann. Hier im Beispiel entspricht der Wert der Aktivität \(A\), die die Probe zum Zeitpunkt \(t=0\) besaß. Bei einer umgekehrt proportionalen Zuordnung gibt es hingegen hier keinen sinnvollen Wert.
Optional: Grafisch Näherungswerte bestimmen
Durch die im Diagramm eingetragenen Messwerte kannst du eine Ausgleichskurve zeichnen (vgl. Abb. 2.2). Mit Hilfe dieser Ausgleichskurve kannst Du denn Schnittpunkt mit der Hochachse ermitteln. Dies liefert dir eine Näherung für die Aktivität der Probe zum Zeitpunkt \(t=0\), also den Startwert. Auch die sog. Halbwertszeit kannst du mit dem Graphen näherungsweise bestimmen. Suche dazu ein geeignetes Wertepaar, bei dem sich die Aktivität gerade halbiert hat, und ermittle die dafür benötigte Zeitspanne (vgl. Abb. 2.3).
Wachstums-Regression mit GTR oder Tabellenkalkulation
3. Durchführung der Regression
Nun lässt du das System eine Regression durchführen (siehe Abb. 3.1). Dabei musst du das Regressionsmodell einstellen. In GeoGebra kannst du hier das Modell "Wachstum" wählen (vgl. Abb. 3.2), was von einer Funktion der Form \(y=a\cdot b^x\) ausgeht.
Hinweis: In einigen anderen Systemen (wie z.B. Excel) kannst du nur exponentielle Regression wählen. Dies liefert dir die zugehörige Funktion als \(e\)-Funktion. Mehr dazu weiter unten im Artikel.
4. Startwert und Wachstumsfaktor ermitteln
Die Regression liefert dir Werte für die Parameter \(a\) und \(b\) im Funktionsterm, hier \(a=5{,}0\) und \(b=0{,}81\) (vgl. Abb. 3.2). Dabei ist \(a=5{,}0\) der Startwert, also die Aktivität, die die Probe zu Beginn hatte. \(b=0{,}81\) ist der Wachstumsfaktor. Da \(b<1\) ist, handelt es sich um eine exponentielle Abnahme. Dies ist logisch, da die Aktivität eines radioaktiven Stoffes mit der Zeit in der Regel weniger wird, da Teile in stabile Elemente übergehen. Die ermittelte, zu den Beispielmesswerten am besten passende Exponentialfunktion ist somit \(f(x)=5{,}0\cdot 0{,}81^x\). Das diese Funktion gut zu dem Messwerten passt zeigt auch der Wert des Bestimmtheitsmaßes von \(R^2=0{,}999\), der sehr nahe bei 1 liegt. Anschließend zeichnet GeoGebra diese Funktion auch als Trendlinie ins Diagramm ein (siehe Abb. 3.3).
5. Halbwertszeit ermitteln
In einer Halbwertszeit nimmt der Wert der Funktion, hier im Beispiel der Aktivität, auf die Hälfte des ab. Mathematisch ausgedrückt bedeutet dies \[b^x=\frac{1}{2} \quad \text{ bzw. im Beispiel: }\quad 0{,}81^x=\frac{1}{2}\] wobei \(x\) die Halbwertszeit ist. Die Einheit der Halbwertszeit ist hier Sekunden, da die Zeit in der Messwerttabelle in Sekunden angegeben ist. Diese Exponentialgleichung kannst du entweder mit dem Logarithmus zur Basis \(b\) (siehe (1)) oder mit dem natürlichen Logarithmus (siehe (2)) lösen:\[x=\log_{b}{\frac{1}{2}} \quad\text{ bzw. im Beispiel: }\quad x=\log_{0{,}81}{\frac{1}{2}}=3{,}3\quad (1)\]\[x=\frac{-\ln{2}}{\ln{b}} \quad \text{ bzw. im Beispiel: }\quad x=\frac{-\ln{2}}{\ln{0{,}81}}=3{,}3\quad (2)\]
Anders als in der Regression mit \(e\)-Funktion kannst du die sog. Zerfallskonstante \(\lambda\) hier nicht direkt ablesen, sondern muss noch etwas rechnen, um sie zu erhalten. Es gilt\[{e^{-\lambda \cdot x}} = {b^x} \Leftrightarrow -\lambda \cdot x = x \cdot \ln \left( b \right) \Leftrightarrow \lambda = -\ln \left( b \right)\]In unserem Beispiel also \(\lambda=-\ln\left(0{,}81\right)=0{,}21\,\rm{\frac{1}{s}}\).
Exponentielle Regression mit GTR oder Tabellenkalkulation
3. Durchführung der Regression
Nun lässt du das System eine Regression durchführen (siehe Abb. 4.1). Dabei musst du das Regressionsmodell einstellen. In GeoGebra kannst du hier das Modell "Exponentiell" wählen (vgl. Abb. 4.2), was von einer Funktion der Form \(y=a\cdot e^{b\cdot x}\) ausgeht.
4. Startwert und Wachstumsfaktor ermitteln
Die Regression liefert dir Werte für die Parameter \(a\) und \(b\) im Funktionsterm, hier \(a=5{,}0\) und \(b=-0{,}22\) (vgl. Abb. 4.2). Dabei ist \(a=5{,}0\) der Startwert, also die Aktivität, die die Probe zu Beginn hatte. \(b=-0{,}22\) ist hier der negative Wert der sog. Zerfallskonstanten \(\lambda\). Da \(b<0\) ist, handelt es sich um eine exponentielle Abnahme. Dies ist logisch, da die Aktivität eines radioaktiven Stoffes mit der Zeit in der Regel abnimmt. Die ermittelte, zu den Beispielmesswerten am besten passende \(e\)-Funktion ist somit \(f(x)=5{,}0\cdot e^{-0{,}22\cdot x}\). Anschließend zeichnet GeoGebra diese Funktion auch als Trendlinie ins Diagramm ein (siehe Abb. 4.3).
5. Halbwertszeit ermitteln
Aus der Regression mit dem exponentiellen Modell kannst du die Zerfallskonstante \(\lambda\) direkt ablesen. Es ist \(\lambda =-b\) also in unserem Beispiel \(\lambda= 0{,}22\,\rm{\frac{1}{s}}\). Für die Halbwertszeit gilt \[T_{1/2} = \frac{\ln \left( 2 \right)}{\lambda}\quad\text{ also hier im Beispiel: }\quad T_{1/2} = \frac{\ln \left( 2 \right)}{0{,}22\,\frac{1}{{\rm{s}}}}=3{,}2\,\rm{s}\]Hinweis: Die minimale Abweichung der Halbwertszeit kommt durch Rundungsfehler bei der Verwendung der unterschiedlichen Regressionsmodelle zustande.