In der Aufgabe "Eine Fahrt zu α-Centauri" dauert der gleichförmige Flug einer Rakete von der Erde zum nächstgelegenen Sternensystem α-Centauri für den auf der Erde sitzenden Beobachter \(\Delta t = 5{,}4\,\rm{a}\), für den mitfliegenden Astronauten jedoch nur \(\Delta t'=3{,}2\,\rm{a}\). Erdbewohner und Astronaut gehen dabei von der gleichen Relativgeschwindigkeit \(v=0{,}8\cdot c\) aus. Wie ist es da möglich, dass sie unterschiedliche Zeiten beobachten?
Mathematische Betrachtung
Der Erdbewohner schreibt: \[v = \frac{\Delta x}{\Delta t}\quad(1)\]Der Astronaut schreibt: \[v = \frac{\Delta x'}{\Delta t'}\quad(2)\]
Setzt man \(\left(1\right)\) und \(\left(2\right)\) gleich, so erhält man:\[\frac{\Delta x'}{\Delta t'} = \frac{\Delta x}{\Delta t}\Rightarrow \Delta x' = \Delta x \cdot \frac{\Delta t'}{\Delta t}\] und mit der Formel für die Zeitdilatation folgt:\[\Delta x' = \Delta x \cdot \frac{\Delta t \cdot \sqrt{1 - \left(\frac{v}{c}\right)^2}}{\Delta t}\Rightarrow\Delta x' = \Delta x \cdot \sqrt{1 - \left(\frac{v}{c}\right)^2}\]
Der Astronaut muss also für die Entfernung Erde - Alpha-Centauri von einer kürzeren Strecke ausgehen. Man spricht von der Längenkontraktion.
Die Längenkontraktion
Bewegt sich ein Beobachter an einer Strecke der Länge \(\Delta x\) mit der Geschwindigkeit \(v\) vorbei, so ist die Strecke für ihn auf den Wert \(\Delta x'\) verkürzt (Längenkontraktion):
\[\Delta x' = \Delta x \cdot \sqrt{1 - \left(\frac{v}{c}\right)^2}\]
Hinweis: Die Längenkontraktion findet nur in Bewegungsrichtung statt. Strecken senkrecht zur Bewegungsrichtung behalten ihre Länge auch für den bewegten Beobachter bei.
Veranschaulichung
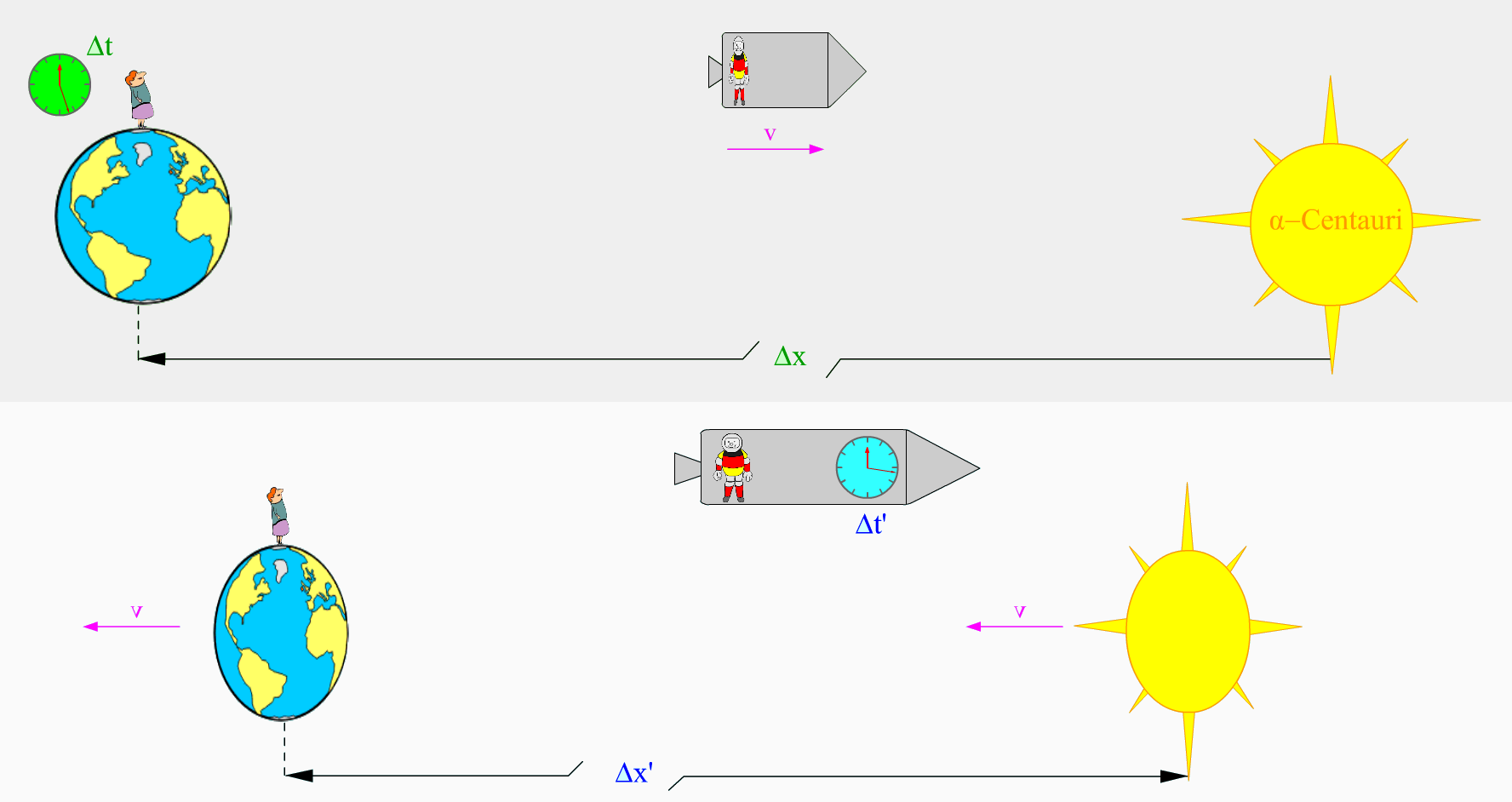
Die Verhältnisse für den Flug von der Erde zu Alpha-Centauri sind in Abb. 1 illustriert:
Das obere Bild zeigt, wie ein Erdbewohner beobachtet: Er stellt für die Entfernung der Himmelskörper die Strecke \(\Delta x\) fest und misst als Zeitspanne zwischen den Ereignissen "Start" und "Ankunft" die Zeit \(\Delta t\). Die Ablesung erfolgt dabei an räumlich verschiedenen Uhren. Die Rakete würde der Erdbewohner verkürzt wahrnehmen.
Das untere Bild zeigt, wie ein mitfliegender Astronaut beobachtet: Er stellt für die Entfernung der Himmelskörper die Strecke \(\Delta x'< \Delta x\) fest und misst als Zeitspanne zwischen den Ereignissen "Start" und "Ankunft" die Zeit \(\Delta t'<\Delta t\). Die Ablesung erfolgt hier an einer Uhr. Die Erde sieht der Astronaut in Bewegungsrichtung geschrumpft.