James WATT (1736 - 1819) produzierte zusammen mit Matthew BOULTON (1728 - 1809) in einer gemeinsamen Firma Dampfmaschinen. 1788 entdeckte BOULTON den Fliehkraftregler beim Windmühlenbau und setzte ihn zur Drehzahlregelung der Dampfmaschinen ein.
Aufbau und Funktionsweise
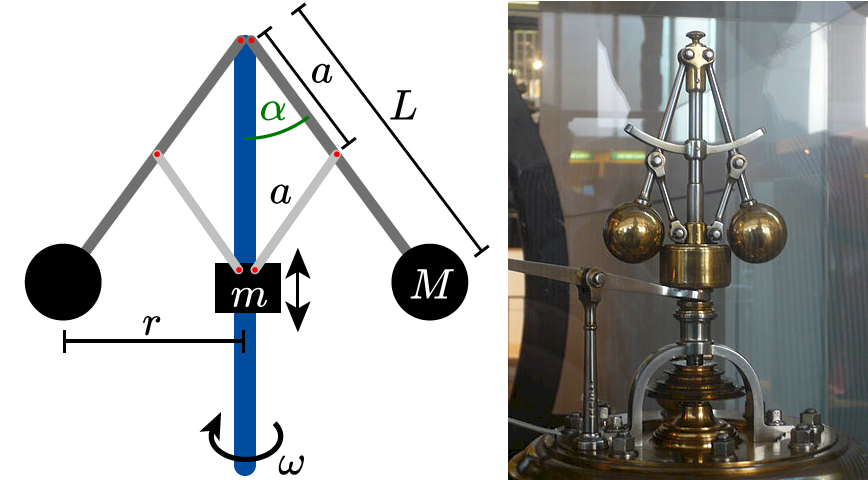
Die Funktionsweise eines Fliehkraftreglers ist wie folgt: An einer mit der Winkelgeschwindigkeit \(\omega\) rotierenden Drehachse sind zwei Hebel der Länge \(L\) beweglich befestigt, an deren Enden sich zwei Kugeln der Masse \(M\) befinden. Im Abstand \(a\) vom Drehpunkt sind an den Hebeln zwei weitere kurze Stangen der Länge \(a\) befestigt, die einen auf der Achse gleitenden Ring der Masse \(m\) heben oder senken. Je größer die Winkelweite \(\alpha \) zwischen Achse und Hebel, desto höher steigt der Ring, der bei der Dampfmaschine die Dampfzufuhr regelt.
Simulation eines Fliehkraftreglers
Versuch und mathematische Beschreibung im Video
Mathematische Betrachtung bei Vernachlässigung von \(m\)
Vernachlässigst du die Gewichtskraft der inneren Masse \(m\) so wirkt auf die Anordnung die Gewichtskraft \({{\vec F}_{{\rm{G}}{\rm{,}}M}}\) Kugelmassen und eine durch die Metallstangen aufgebrachte Kraft \({{\vec F}_{\rm{S}}}\). Gemeinsam, also vektoriell addiert müssen beide gerade die für die Kreisbahn der rotierenden Anordnung notwendige Zentripetalkraft \({{\vec F}_{{\rm{ZP}}}}\) bilden. Somit gilt für den sich einstellenden Winkel \(\alpha\) im Gleichgewichtsfall:\[\frac{{\sin \left( \alpha \right)}}{{\cos \left( \alpha \right)}} = \tan \left( \alpha \right) = \frac{{{F_{{\rm{ZP}}}}}}{{{F_{{\rm{G}}{\rm{,}}M}}}} = \frac{{M \cdot {\omega ^2} \cdot L \cdot \sin \left( \alpha \right)}}{{M \cdot g}}\]\[\Rightarrow \cos \left( \alpha \right) = \frac{g}{{{\omega ^2} \cdot L}}\]
Aufgabe
Erläutere, welche Kräfte im nicht rotierenden Bezugssysstem auf \(M\) wirken, wenn du Gewichtskraft der Masse \(m\) vernachlässigst.
Berechne die Winkelweite \(\alpha \) unter Vernachlässigung von \(m\) für \(\omega = 8\,\frac{1}{{\rm{s}}}\), \(M=1{,}5\,\rm{kg}\) und \(L=17{,}5\,\rm{cm}=0{,}175\,\rm{m}\).
Zusatzaufgabe: Erläutere, welche Kräfte im rotierenden Bezugssysstem auf \(M\) wirken, wenn du Gewichtskraft der Masse \(m\) vernachlässigst.
Betrachtung unter Einbezug von \(m\)
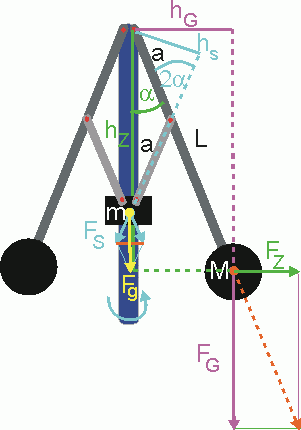
Wir betrachten im rotierenden Bezugssystem das Gleichgewicht der Drehmomente. Das linksdrehende Moment wird durch die Zentrifugalkraft der Masse \(M\) bewirkt: \[{M_{\rm{L}}} = {F_{{\rm{ZP}}}} \cdot {h_{\rm{Z}}}\] Mit \({F_{{\rm{ZP}}}} = M \cdot {\omega ^2} \cdot L \cdot \sin \left( \alpha \right)\) und \({{h_Z} = L \cdot \cos \left( \alpha \right)}\) ergibt sich dann \[{M_{\rm{L}}} = M \cdot {\omega ^2} \cdot L \cdot \sin \left( \alpha \right) \cdot L \cdot \cos \left( \alpha \right)\] Das rechtsdrehende Moment wird durch die Gewichtskraft der Masse \(M\) und die über die kleine Stange der Länge \(a\) wirkende Gewichtskraft der Masse \(m\) bewirkt: \[{M_{\rm{R}}} = {F_{\rm{G}}} \cdot {h_{\rm{G}}} + {F_{\rm{S}}} \cdot {h_{\rm{S}}}\] Nun gilt \({{F_{\rm{G}}} = M \cdot g}\) und \({h_{\rm{G}}} = L \cdot \sin \left( \alpha \right)\) sowie \[{\cos \left( \alpha \right) = \frac{{\frac{1}{2} \cdot m \cdot g}}{{{F_{\rm{S}}}}} \Leftrightarrow {F_{\rm{S}}} = \frac{{m \cdot g}}{{2 \cdot \cos \left( \alpha \right)}}}\] und \[{h_{\rm{S}}} = a \cdot \sin \left( {2 \cdot \alpha } \right) = a \cdot 2 \cdot \sin \left( \alpha \right) \cdot \cos \left( \alpha \right)\] Damit ergibt sich \[{M_{\rm{R}}} = M \cdot g \cdot L \cdot \sin \left( \alpha \right) + \frac{{m \cdot g}}{{2 \cdot \cos \left( \alpha \right)}} \cdot a \cdot 2 \cdot \sin \left( \alpha \right) \cdot \cos \left( \alpha \right) = \left( {M \cdot L + m \cdot a} \right) \cdot g \cdot \sin \left( \alpha \right)\] Gleichsetzen von \({M_{\rm{L}}}\) und \({M_{\rm{R}}}\) ergibt \[{M_{\rm{L}}} = {M_{\rm{R}}} \Leftrightarrow M \cdot {\omega ^2} \cdot {L^2} \cdot \sin \left( \alpha \right) \cdot \cos \left( \alpha \right) = \left( {M \cdot L + m \cdot a} \right) \cdot g \cdot \sin \left( \alpha \right)\]\[\Leftrightarrow \cos \left( \alpha \right) = \frac{{\left( {M \cdot L + m \cdot a} \right) \cdot g}}{{M \cdot {\omega ^2} \cdot {L^2}}}\]Auf dieser Formel basiert auch die oben dargestellte Simulation.