Aufbau und Durchführung

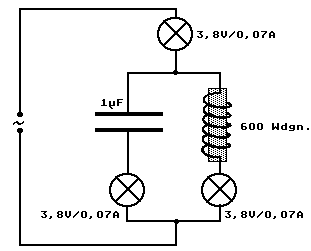
Man regelt die Frequenz von niederen Werten langsam hoch und wieder zurück und betrachtet die Lämpchen.
Beobachtung
-
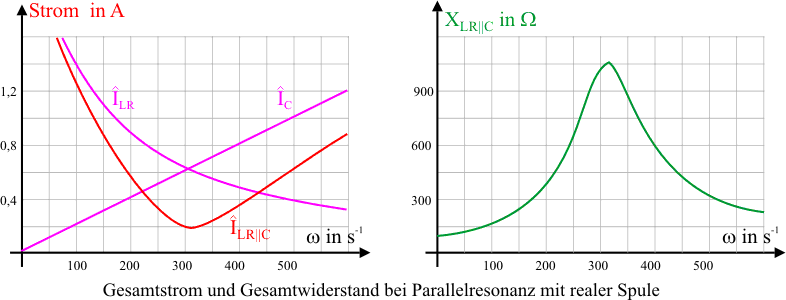
Bei Frequenzen unterhalb der Resonanzfrequenz leuchtet das Lämpchen im Hauptkreis deutlich auf. In der Parallelschaltung fließt der Strom hauptsächlich durch die Spule.
-
Im Resonanzfall erreicht die Helligkeit des Lämpchens im Hauptkreis ein Minimum. Die Lämpchen im Spulen- und Kondensatorkreis leuchten gleich hell.
-
Für Frequenzen oberhalb der Resonanzfrequenz steigt der Strom in der Hauptleitung wieder an. Das Lämpchen im Kondensatorzweig ist heller als das im Spulenzweig.
-
Bei der obigen Anordnung können die Ströme in den Teilzweigen sehr viel größere Amplituden erreichen als der Strom in der Hauptleitung. Man spricht daher beim Parallelkreis auch von Stromresonanz.
Erklärung: Zeigerdiagramm bei idealer Spule (R = 0)
Es lohnt sich, das zur Parallelresonanz gehörige Zeigerdiagramm zu betrachten. Dabei sei zunächst der einfache Fall einer idealen Spule angenommen, die parallel zu einem Kondensator geschaltet ist.
Der Aufbau des Zeigerdiagramms geschieht wie folgt:
-
Man beginnt das Diagramm mit der elektrischen Größe, die beiden Elementen (Spule und Kondensator) gemeinsam ist. Bei der Parallelschaltung ist dies die Spannung.
-
Der Strom durch die Spule hinkt der Spannung um 90° nach.
-
Der Strom durch den Kondensator eilt der Spannung um 90° voraus.
-
Der resultierende Strom ergibt sich durch Vektoraddition der beiden bisher eingezeichneten Strompfeile.
Was geschieht nun bei der Änderung der Kreisfrequenz \(\omega\)?
-
Bei niederen Frequenzen ist der Wechselstromwiderstand der Spule kleiner als der des Kondensators. Es gilt\[{{\hat I}_L} > {{\hat I}_C}\]und der Gesamtstrom hinkt der Spannung um 90° nach.
-
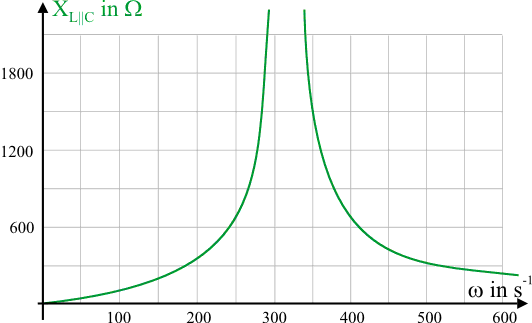
Im Resonanzfall sind die beiden Ströme durch Spule und Kondensator gleich groß. Es gilt\[{{\hat I}_L} = {{\hat I}_C}\]Der Gesamtstrom im Hauptzweig hat bei der Idealisierung (R = 0) den Wert Null, da die beiden Teilströme eine Phasenverschiebung von 180° haben. Der Widerstand des Parallelkreises ist in diesem Fall unendlich groß, daher spricht man auch von einem Sperrkreis.
-
Wird die Resonanzfrequenz überschritten, so übersteigt der Kondensatorstrom den Spulenstrom. Der Gesamtstrom eilt dann der Spannung um 90° voraus. Es gilt\[{{\hat I}_L} < {{\hat I}_C}\]
Mit Hilfe des Zeigerdiagramms lässt sich der Gesamtwiderstand des Parallelkreises aus Kondensator und idealer Spule sehr schnell berechnen. Es gilt\[{{\hat I}_{L\parallel C}} = \left| {{{\hat I}_L} - {{\hat I}_C}} \right| = \left| {\frac{{{{\hat U}_{L\parallel C}}}}{{\omega \cdot L}} - {{\hat U}_{L\parallel C}} \cdot \omega \cdot C} \right| = {{\hat U}_{L\parallel C}} \cdot \left| {\frac{1}{{\omega \cdot L}} - \omega \cdot C} \right|\]und damit\[{X_{L\parallel C}} = \frac{{{{\hat U}_{L\parallel C}}}}{{{{\hat I}_{L\parallel C}}}} = \frac{{{{\hat U}_{L\parallel C}}}}{{{{\hat U}_{L\parallel C}} \cdot \left| {\frac{1}{{\omega \cdot L}} - \omega \cdot C} \right|}} = \frac{1}{{\left| {\frac{1}{{\omega \cdot L}} - \omega \cdot C} \right|}}\]Damit ergibt sich folgendes \(\omega\)-\({X_{L\parallel C}}\)-Diagramm:
Verwendet man eine reale Spule, so stellt die Konzeption des Zeigerdiagramms und die Widerstandsberechnung höhere Ansprüche, die nicht zum Pflichtstoff gehören. Wenn du dich dennoch dafür interessierst, so kannst du gerne weiterlesen.
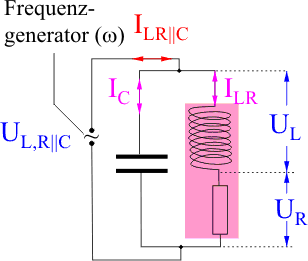
Bei der Parallelresonanz mit der realen Spule muss man sich im Spulenzweig noch einen ohmschen Widerstand in Serie zur idealen Spule geschaltet denken.
Hier ist nun auf den ersten Blick nicht ganz klar, mit welcher elektrischen Größe man das Zeigerdiagramm beginnen soll. Ein guter Tipp ist der Beginn mit dem Zeiger des Stroms, der durch \(L\) und durch \(R\) fließt.
Außer dem Gesamtstrom lassen sich alle Zeigerlängen relativ einfach berechnen. Für die Berechnung des Gesamtstroms aus dem Strom durch den Kondensator IC und dem Strom im Spulenzweig ILR muss man den Kosinussatz benutzen.
Nach einigen trigonometrischen Umformungen - auf die hier nicht eingegangen wird - gelangt man für den Gesamtwiderstand der Schaltung zum Ergebnis\[{X_{L\parallel C}} = \frac{{\sqrt {{R^2} + {{\left( {\omega \cdot L} \right)}^2}} }}{{\omega \cdot C \cdot \sqrt {{R^2} + {{\left( {\omega \cdot L - \frac{1}{{\omega \cdot C}}} \right)}^2}} }}\]Für die Resonanzfrequenz beim Phasenwinkel φ = 0 ergibt sich\[\omega = \frac{1}{{\sqrt {L \cdot C} }} \cdot \sqrt {1 - {R^2} \cdot \frac{C}{L}} \]
Die folgenden Abbildungen zeigen den Verlauf des Gesamtwiderstands und des Gesamtstroms bei der Parallelresonanz mit realer Spule. Dabei wurden folgende Werte zu Grunde gelegt: Amplitunde der Gesamtspannung 200V, R = 100Ω, C = 10,0μF und L = 1,00H. Beachte, dass der Gesamtwiderstand im Resonanzfall - im Gegensatz zur Überlegung mit idealer Spule - nicht mehr ins Unendliche steigt. Am Verlauf der Stromkurven (Minimum des Gesamtstroms) kann man den Begriff "Stromresonanz" verstehen.