Aufbau und Durchführung
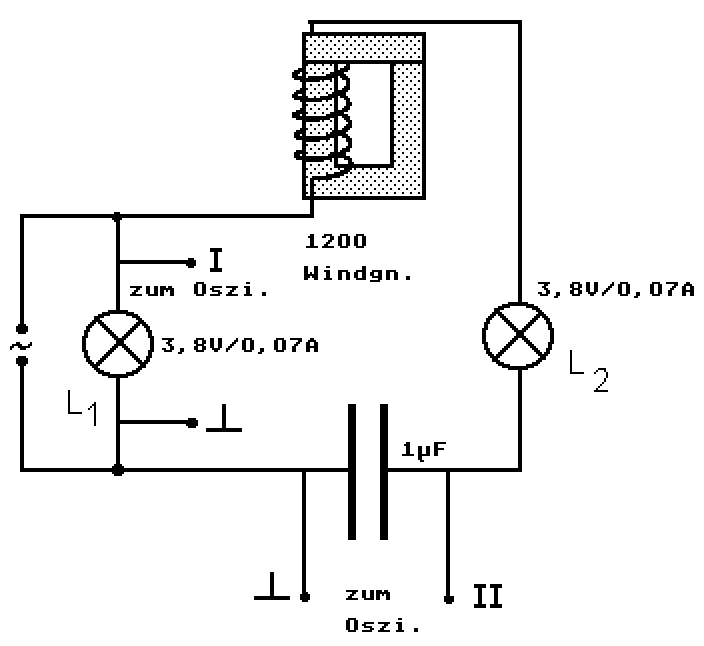
Man schließt an den Ausgang des Sinusgenerators eine Serienschaltung aus Kondensator und Spule und einer empfindlichen Glühlampe \(\rm{L_2}\) an. Parallel dazu wird an den Ausgang eine zweite gleichartige Glühlampe \(\rm{L_1}\) angeschlossen, damit man erkennt, dass die Ausgangsspannung während der Variation der Frequenz konstant bleibt. Beginnend bei niederen Frequenzen (ca. \(100 \rm{Hz}\)) wird die Frequenz gesteigert.
Beobachtung
Lampe \(\rm{L_2}\) leuchtet am Anfang kaum. Bei einer bestimmten Frequenz leuchtet Lampe \(\rm{L_2}\) hell auf, bei weiterer Steigerung der Frequenz nimmt die Helligkeit von \(\rm{L_2}\) wieder ab.
Mit dem Oszilloskop kann man die Ausgangsspannung des Sinusgenerators zwischen Masse (\( \bot \)) und Abgriff 1 an Kanal I bebachten und die Spannung am Kondensator zwischen Masse (\( \bot \)) und Abgriff II an Kanal II beobachten.
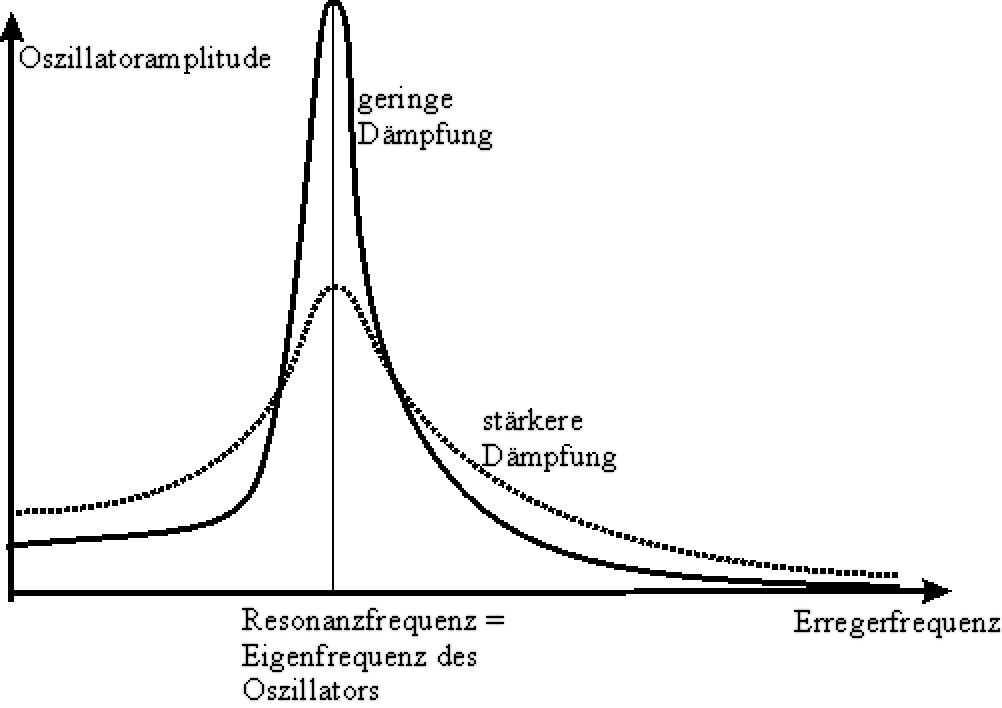
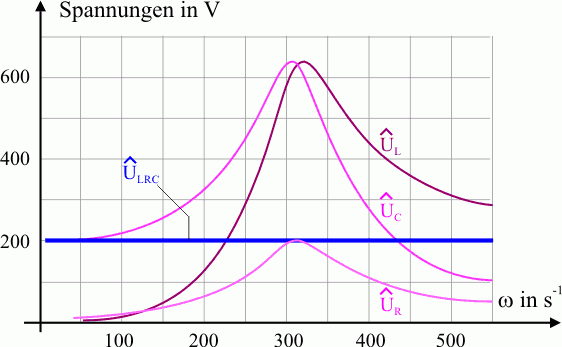
Die Resonatoramplitude (hier die Spannung am Kondensator) ist im Resonanzfall um das etwa 10 fache höher als die Erregeramplitude (Spannung am Generatorausgang). Man spricht daher bei der Serienresonanz auch von der Spannungsresonanz. Der Amplitudenverlauf am Resonator ist rechts dargestellt.
Ergebnis
Die Serienschaltung von Spule und Kondensator stellt also ein schwingungsfähiges System dar, das von außen zu erzwungenen Schwingungen angeregt werden kann. Im Folgenden findest du die Theorie für die Berechnung des Gesamtwiderstandes einer Serienschaltung; sie ist aber eher für mathematisch Interessierte gedacht.
Die Behandlung der Serienresonanz mit dem Zeigerdiagramm ist im Vergleich zur Parallelresonanz einfacher. Daher gehen wir sofort zum komplexeren Fall, bei dem eine reale Spule verwendet wird.
Wenn du wissen willst, wie das Zeigerdiagramm bzw. die wesentlichen Formeln bei Verwendung der idealen Spule aussehen würden, so brauchst du im Zeigerdiagramm dem zum Widerstand gehörenden Zeiger nur die Länge Null geben bzw. in den Formeln R = 0 setzen.
Den Zusammenhang zwischen Gesamtspannung \({{\hat U}_{LRC}}\) und Gesamtstrom \({{\hat I}_{LRC}}\) (also den Gesamtwiderstand) erhält man wie folgt: Aus\[{{\hat U}_R} = R \cdot {{\hat I}_{LRC}}\]und\[\left| {{{\hat U}_L} - {{\hat U}_C}} \right| = \left| {\omega \cdot L \cdot {{\hat I}_{LRC}} - \frac{1}{{\omega \cdot C}} \cdot {{\hat I}_{LRC}}} \right| = \left| {\omega \cdot L - \frac{1}{{\omega \cdot C}}} \right| \cdot {{\hat I}_{LRC}}\]erhält man nach dem Satz von PYTHAGORAS für die Gesamtspannung\[{{\hat U}_{LRC}} = \sqrt {{{\left| {{{\hat U}_L} - {{\hat U}_C}} \right|}^2} + {{\hat U}_R}^2} = {{\hat I}_{LRC}} \cdot \sqrt {{{\left( {\omega \cdot L - \frac{1}{{\omega \cdot C}}} \right)}^2} + {R^2}} \]Hieraus ergibt sich \[{X_{LRC}} = \frac{{{{\hat U}_{LRC}}}}{{{{\hat I}_{LRC}}}} = \frac{{{{\hat I}_{LRC}} \cdot \sqrt {{{\left( {\omega \cdot L - \frac{1}{{\omega \cdot C}}} \right)}^2} + {R^2}} }}{{{{\hat I}_{LRC}}}} =\sqrt {{{\left( {\omega \cdot L - \frac{1}{{\omega \cdot C}}} \right)}^2} + {R^2}} \]und\[{{\hat I}_{LRC}} = \frac{{{{\hat U}_{LRC}}}}{{{X_{LRC}}}} = \frac{{{{\hat U}_{LRC}}}}{{\;\sqrt {{{\left( {\omega \cdot L - \frac{1}{{\omega \cdot C}}} \right)}^2} + {R^2}} }}\]
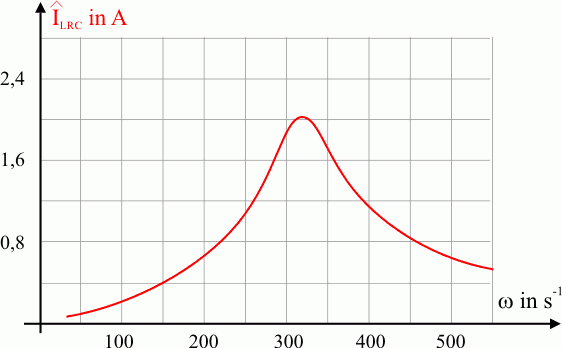
Für die folgenden Diagramme wurden die Werte \({{{\hat U}_{LRC}} = 200{\rm{V}}}\), \({R = 100\Omega }\), \({C = 10,0{\rm{\mu F}}}\) und \(L=1,00\rm{H}\) zu Grunde gelegt.
Bei der Resonanzfrequenz (ca. \(3{,}2 \cdot 10^2 \, \rm{s}^{-1}\) ) zeigt der Gesamtstrom ein Maximum.
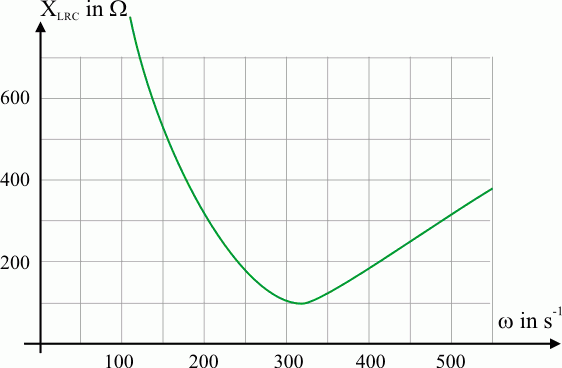
Entsprechend dem Strommaximum bei der Resonanzfrequenz zeigt der Widerstand bei dieser Frequenz ein Minimum. Der Wert des Minimums entspricht dem Wert des ohmschen Widerstands (im Beispiel \(100\Omega\)).
Das Spannungsdiagramm zeigt, dass bei einer Generatorspannung mit der Amplitude \(200\rm{V}\) an den Elementen Spule und Kondensator erheblich höhere Spannungen (im Beispiel mehr als \(600 \rm{V}\)) auftreten können (Spannungsresonanz).