Versuchsidee
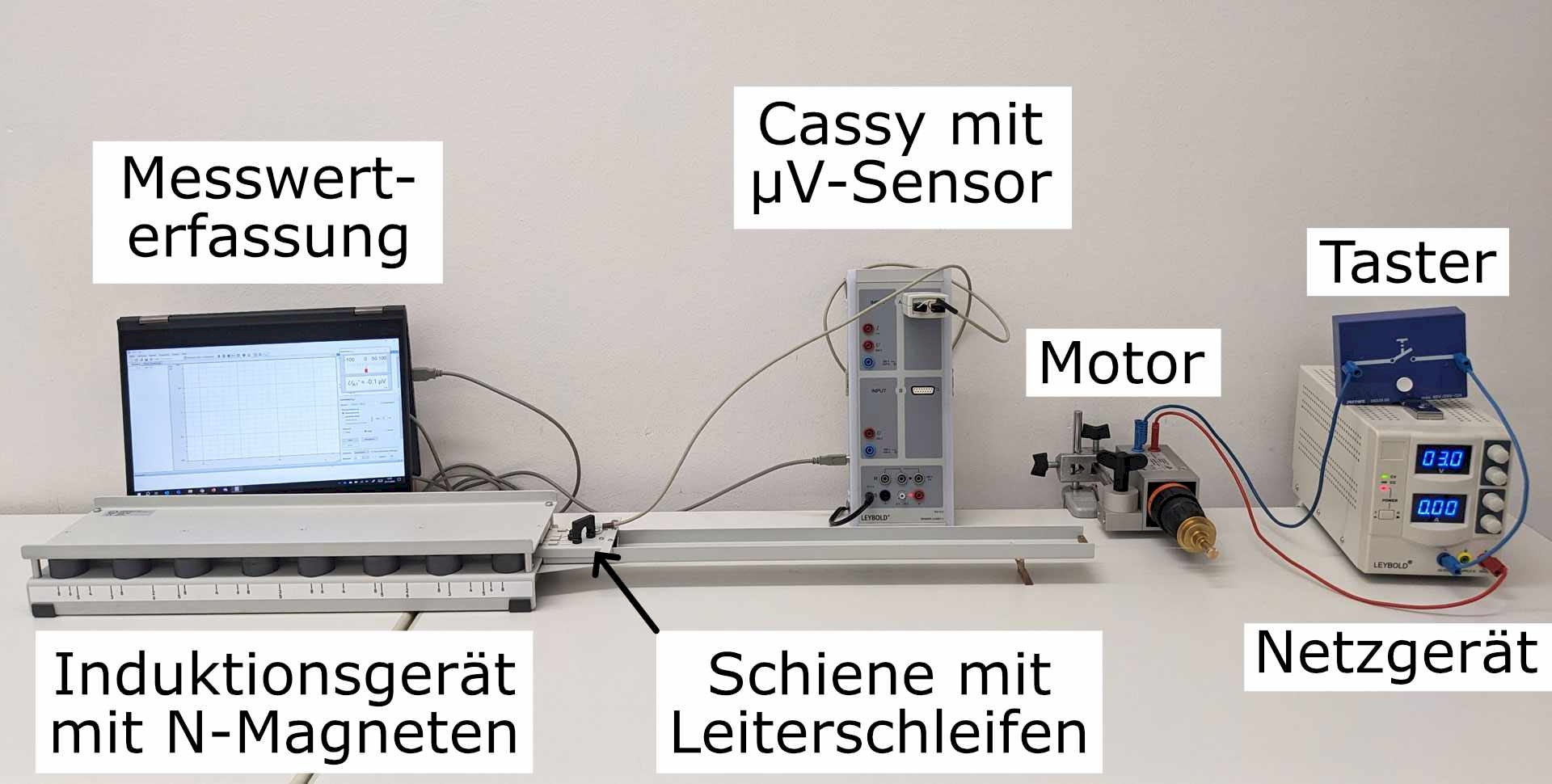
Leiterschleifen mit verschiedenen Breiten \(b\) werden mit der Geschwindigkeit \(v\) durch ein homogenes Magnetfeld \(B\) bewegt. An den Enden der Leiterschleife entsteht dabei eine kleine Induktionsspannung \(U_{\rm{ind}}\), die mit einem Mikrovoltmeter gemessen wird (vgl. Abb. 1).
Im Versuch können alle drei relevanten Größen variiert werden: Die Breite \(b\) der Leiterschleife, die Geschwindigkeit \(v\), mit der die Schleife durch das Magnetfeld gezogen wird und die Stärke des Magnetfeldes \(B\).
Material für Realexperiment
- Induktionsgerät mit Leiterschleifen, passende Magnete und Rutschkupplung
- Cassy mit Mikrovolt-Sensor / Alternativ: Mikrovoltverstärker
- Experimentiermotor mit passendem Netzgerät
- Angelschnur
- evtl. Schalter oder Taster zur Motorsteuerung
Alternative Simulation
Steht das notwendige Experimentiermaterial nicht zur Verfügung, kann auch die hier verfügbare Simulation des Experimentes eingesetzt werden. Tipp: Der Graph der magnetische Flussdichte kann bei Bedarf ausgeblendet werden.
Wir danken Thomas Kippenberg (https://www.kippenbergs.de) für die Erlaubnis, diese Simulation auf LEIFIphysik zu nutzen.
Versuchsaufbau
Das Induktionsgerät wird auf einem langen Experimentiertisch ausgeklappt und entsprechend den Markierungen mit N Paaren Scheibenmagneten bestückt (vgl. Abb. 3.1). Nun die Schiene mit den verschiedenen Leiterschleifen herausziehen (Abb. 3.2) und mittels einer dünnen Angelschnur durch die Führung mit der am Motor befestigten Rutschkupplung verbinden (Abb. 3.3). Mit der Steckverbindung auf der Schiene kann die Leiterschleife ausgewählt werden, an der die Induktionsspannung gemessen werden soll. Die von der Schiene kommenden Anschlüsse zur Spannungsmessung werden an den µV-Sensor des Cassy-Systems angeschlossen (Abb. 3.4). Alternativ kann auch ein Mikrovolt-Messverstärker mit Anzeige genutzt werden. Achtung: Beim manuellen Bewegen und beim zurückschieben der Leiterschleife immer den Trenn-Taster der Spannungsmessung an der Schiene drücken. Dies schützt Sensor bzw. Messverstärker vor Überspannung.
Der Motor selbst ist mittels Klemmen am Tisch fixiert und an ein passendes Netzgerät angeschlossen (Abb. 3.4). Optional kann in diesen Stromkreis ein Taster oder Schalter eingebaut werden, um den Motor jeweils mit unveränderter Spannung betreiben zu können. Ansonsten muss das Netzgerät immer wieder ein- und ausgeschaltet werden. Um die Leiterschleifen mit unterschiedlichen Geschwindigkeiten bewegen zu können, muss die Angelschnur an der Rutschkupplung jeweils so geführt werden, dass sie sich auf dem Abschnitt mit gewünschtem Radius aufwickelt (vgl. Abb. 3.5-3.7). Bei der Durchführung darauf achten, dass sich die Schnur wie in Abb. 3.8 nebeneinander aufwickelt.
Die Messwerterfassung durch Cassy kann entweder genutzt werden, die aktuell gemessene Induktionsspannung als Zahlenwert auszugeben, oder um jeweils die \(t\)-\(U_{\rm{ind}}\) bei der Bewegung aufzuzeichnen. Im zweiten Fall bietet sich der Einsatz eines Triggers zum automatischen Start der Messwertaufnahme bei ansteigender Induktionsspannung an.
Versuchsdurchführung
Auf der Metallschiene befinden sich drei Leiterschleifen mit verschiedenen Breiten \(b\). Durch entsprechende Positionierung des Steckkontaktes (siehe Abb. 3.2) wird die Leiterschleife ausgewählt, an der die Induktionsspannung \(U_{\rm{ind}}\) gemessen wird.
Die Schiene mit den Leiterschleifen wird mit Hilfe eines Motors durch ein homogene Magnetfeld gezogen. Die Geschwindigkeit \(v\) der Leiterschleifen wird bei fester Betriebsspannung des Motors über die Übersetzung an der Rutschkupplung reguliert. Die drei Durchmesser der Kupplung sind gerade so gewählt sind, dass der Versuch mit \(v_0\), \(2\cdot v_0\) und \(4\cdot v_0\) durchgeführt werden kann.
Das Magnetfeld wird durch N Paare von Scheibenmagneten erzeugt, die links und rechts des Metallrahmens angeordnet werden. Zwischen den Polschuhen oben und unten herrscht dann ein annähernd homogenes Magnetfeld, dessen Stärke durch die Zahl der Scheibenmagnet-Paare variiert werden kann.
Beobachtung
a) Abhängigkeit der Induktionsspannung von der Geschwindigkeit der Leiterschleife (N = 8; b = 4,0cm)
| v in relativen Einheiten | 1·v0 | 2·v0 | 4·v0 |
| U in μV | 50 | 101 | 204 |
b) Abhängigkeit der Induktionsspannung von der Breite der Leiterschleife (N = 8; v = 4·v0)
| b in cm | 4,0 | 3,0 | 2,0 |
| U in μV | 204 | 146 | 108 |
c) Abhängigkeit der Induktionsspannung von der Stärke des Magnetfeldes (b = 4,0cm; v = 4·v0)
Es wird davon ausgegangen, dass die Stärke des Magnetfeldes proportional zur Zahl N der Scheibenmagneten-Paare ist.
| N | 8 | 6 | 5 | 4 | 3 | 2 |
| U in μV | 204 | 160 | 138 | 108 | 80 | 54 |
Auswertung
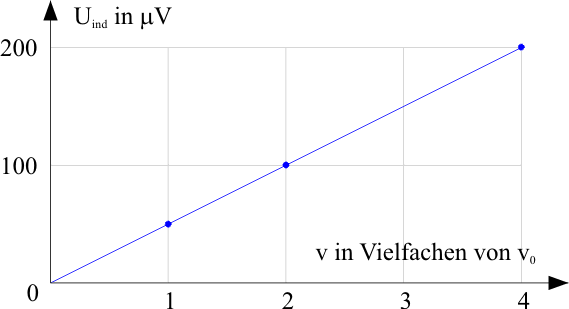
| a) Abhängigkeit der Induktionsspannung von der Geschwindigkeit der Leiterschleife (N = 8; b = 4,0cm) | |||||||||
\( U_\text{ind} \sim v \) bei b und B konstant |
 |
||||||||
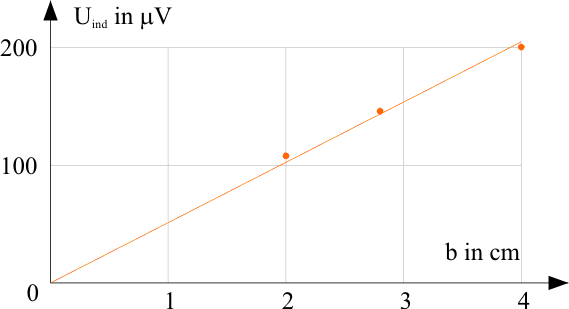
| b) Abhängigkeit der Induktionsspannung von der Breite der Leiterschleife (N = 8; v = 4·v0) | |||||||||
\( U_\text{ind} \sim b \) bei v und B konstant |
 |
||||||||
|
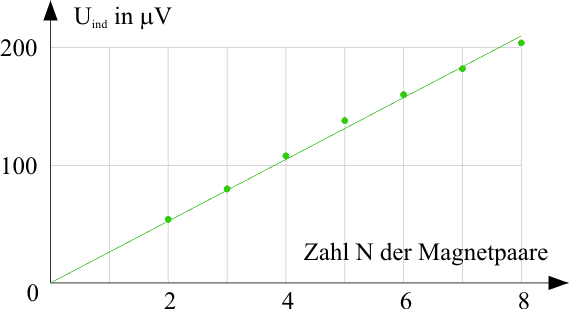
c) Abhängigkeit der Induktionsspannung von der Stärke des Magnetfeldes (b = 4,0cm; v = 4·v0) |
|||||||||||||||
\(U_\text{ind} \sim B \) bei b und v konstant |
 |
||||||||||||||
Aus den drei Teilergebnissen folgt\[ U_\text{ind} \sim v \cdot b \cdot B \]