Natürlich kannst du das Magnetfeld der Erde mit einer empfindlichen Hallsonde ausmessen und so z.B. den Inklinationswinkel der Feldlinien an deinem Aufenthaltsort bestimmen. Auch in deinem Smartphone ist eine solche Hallsonde verbaut, deren Messwerte du mit der App "Phyphox" auslesen und entsprechend auswerten kannst. "Durchsichtiger" kann jedoch die Bestimmung des Erdmagnetfeldes mit Hilfe einer sich drehenden Induktionsspule sein. Eine solche Anordnung nennt man auch Erdinduktor.
Die Versuchsdurchführung ist je nach vorhandenen Messgeräten auf unterschiedliche Art und Weise durchgeführt werden:
Versuchsdurchführung mit Pasco-System
Versuchsgeräte
- Pasco Spannungsmesser und SparkVue oder Capstone-Software
- einzelne, kleine Helmholtzspule mit \(N=320\) Windungen und \(r=6{,}7\,\rm{cm}\)
- Akkuschrauber, Bohrmaschine oder Experimentiermotor
- Kompass zur Bestimmung der Nord-Süd-Richtung
Versuchsaufbau
Um ein endloses Drehen der Spule zu ermöglichen, ohne dass sich Kabel aufwickeln, muss der Spannungsmesser an der Spule fest fixiert werden. Da beim Pasco-System nur der relativ leichte Sensor befestigt werden muss, ist hier Klebeband ausreichend (vgl. Abb. 1.1-Abb. 1.3). Der Anschluss der Kabel an die Spule kann durch das Klebeband hindurch erfolgen. So vorbereitet kann Spule auf den Experimentiermotor montiert werden. Dieser sollte so aufgebaut und befestigt sein, dass seine Ausrichtung zwischen senkrecht und waagerecht variiert werden kann um die Horizontal- bzw. die Vertikalkomponente des Erdmagnetfeldes zu messen (vgl. Abb. 1.4). Bei der Messung der Vertikalkomponente muss die Drehachse in Nord-Süd-Richtung ausgerichtet werden, um nur diesen Teil zu messen.
Wichtig: Eisenteile in der Nähe der Versuchsanordnung können die Messung beeinflussen. Möglichst etwas Abstand von Tischstreben usw. halten.
Alternativ kann die mit dem Sensor versehene Spule auch in einen Akkuschrauber oder eine Bohrmaschine eingespannt werden (vgl. Abb. 1.5). Die Variante mit Akkuschrauber ermöglicht es die Messung auf im Freien, z.B. auf dem Schulhof durchzuführen, wodurch störende Einflüsse durch Eisenteile in Decken und Wänden vermieden werden. Hier muss bei der Durchführung darauf geachtet werden, die Anordnung möglichst stabil zu halten.
Einstellung der Messsoftware und Versuchsdurchführung
Egal, ob die Messung mit SparkVue oder mit Capstone aufgezeichnet und ausgewertet wird, der Sensor sollte auf den Messbereich ±5 V eingestellt und genullt, die Messrate auf 250 Hz oder mehr angepasst werden. Zusätzlich erleichtert es die Auswertung, wenn zeitbasierte Start und Stoppbedingungen zur Messwertaufnahme eingestellt werden. Eine Startverzögerung von 3 Sekunden und ein Stopp nach 5 Sekunden Messzeit ermöglicht eine gute Aufnahme, sodass später beim Fitten nicht erst ein Bereich ausgewählt werden muss. Alternativ kann eine zweite Person die Messung starten, wenn die Spule mit fester Geschwindigkeit rotiert.
Nun wird die Spule mittels Motor oder Akkuschrauber in senkrechter Position zum Rotieren gebracht, die Messwerte zur Ermittlung der Horizontalkomponente werden aufgenommen und in einem \(t\)-\(U_{\rm{i}}\)-Diagramm dargestellt. Anschließend wird die Rotationsachse um 90° gekippt (Nord-Süd-Ausrichtung beachten) und die Messung wiederholt, um die Vertikalkomponente ermitteln zu können.
Versuchsauswertung
Da sich im Experiment die Winkelweite \(\varphi\) mit der Kreisfrequenz \(\omega\) ändert, d.h. \(\varphi\left( t \right) = \omega \cdot t\) ist, gilt\[{U_{\rm{i}}}\left( t \right) = N \cdot B \cdot A \cdot \omega \cdot \sin \left( \omega \cdot t \right)\]Für die Amplitude \(\hat{U}_{\rm{i}}\) gilt entsprechend \[{U_{\rm{i}}}\left( t \right) = N \cdot B \cdot A \cdot \omega\] Aufgelöst nach der gesuchten Größe \(B\) und mit \(\omega=\frac{2\cdot \pi}{T}\) ergibt sich\[B=\frac{\hat{U}_{\rm{i}}}{N \cdot B \cdot A \cdot \omega}\quad\text{bzw.}\quad B=\frac{\hat{U}_{\rm{i}}\cdot T}{N \cdot B \cdot A \cdot 2\cdot \pi}\]
Durch die aufgenommenen Messwerte wird direkt mit der Messsoftware eine Sinuskurve gefittet. Diese liefert die Kennwerte der gefitteten Sinusfunktion, wobei die Amplitude \(a\) der maximalen Induktionsspannung \(\hat{U}_{\rm{i}}\) und bei SparkVue \(b\) der Umlaufdauer \(T\) entspricht (vgl. Abb. 2.1 und Abb. 2.2). Capstone liefert direkt \(\omega\) (vgl. Abb. 2.3 und Abb. 2.4). Die Verschiebungen in \(x\)- und \(y\)-Richtung sind jeweils unrelevant.
Die Fläche der kreisförmigen Spulen ist \(A=\pi r^2 \Rightarrow A=\pi\left(0{,}067\,\rm{m}\right)^2\).
Die horizontale Komponente des Erdmagnetfeldes erhältst du aus den Messwerten mit senkrecht stehender Spulenachse:\[B_{\rm{h}}=\frac{0{,}00360\,\rm{V}\cdot {0{,}164\,\rm{s}}}{320 \cdot \pi\cdot \left(0{,}067\,\rm{m}\right)^2 \cdot 2\cdot \pi}\approx 21\,\rm{\mu T}\]Die vertikale Komponente erhältst du aus den Messwerten bei waagerecht stehender Spulenachse:\[B_{\rm{v}}=\frac{0{,}00674\,\rm{V}\cdot {0{,}164\,\rm{s}}}{320 \cdot \pi\cdot \left(0{,}067\,\rm{m}\right)^2 \cdot 2\cdot \pi}\approx 39\,\rm{\mu T}\]Die Literaturwerte für Deutschland liegen bei \(B_{\rm{h}}\approx 20\,\rm{\mu T}\) und \(B_{\rm{v}}\approx 44\,\rm{\mu T}\).
Gesamtstärke und Inklinationswinkel
Mit Hilfe dieser beiden Werte kannst du über Pythagoras die gesamte Stärke des Erdmagnetfeldes (Literaturwert: \(B=48\,\rm{\mu T}\) ermitteln (siehe Abb. 3). Es gilt\[{B_{\rm{ges}}} = \sqrt {B_{\rm{h}}^2 + B_{\rm{v}}^2} \Rightarrow {B_{\rm{ges}}} = \sqrt {{{21}^2} + {{39}^2}} \,{\rm{\mu T}} \approx {\rm{44}}\,{\rm{\mu T}}\]
Auch den Inklinationswinkel der Magnetfeldlinien, also den Neigungswinkel zwischen einer zur Erdoberfläche parallelen Ebene und der Feldlinie, kannst du mit Hilfe der beiden Komponenten berechnen. Für den Winkel ergibt sich \[\alpha=\tan^{-1}\left(\frac{39}{21}\right)=62°\]
Versuchsdurchführung mit Cassy-System
Versuchsgeräte
- Mobile-Cassy mit Mikrovolt-Sensor
- einzelne, kleine Helmholtzspule mit \(N=320\) Windungen und \(r=6{,}7\,\rm{cm}\)
- Akkuschrauber, Bohrmaschine oder Experimentiermotor
Versuchsaufbau
Senkrecht ausgerichtet, also zur Messung der Horizontalkomponente des Erdmagnetfeldes kann der Versuch auch gut mit Cassy realisiert werden (siehe Abb. 4.1). Beim Cassy-System müssen, falls kein Bluetooth-Adapter vorhanden, sowohl der Mikrovoltsensor als auch ein Mobile Cassy mit der Spule gemeinsam rotieren. Dazu muss die Halterung der Spule verlängert werden und eine Universalmuffe und Gummiringe oder Kabelbinder sorgen für die Befestigung (siehe Abb. 4.2 und Abb. 4.3). Aufgrund der größeren Masse ist eine Versuchsdurchführung nur senkrecht ausgerichtet gut umzusetzen.
Einstellungen und Durchführung
Das Intervall zwischen zwei Messungen sollte auf \(50\,\rm{ms}\) oder weniger eingestellt werden. Da das Mikrovoltmeter deutlich genauer misst als der Pasco-Sensor, kann die Anordnung hier deutlich langsamer rotieren. Das Einstellungen von Triggern zum Start und Stopp der Messung ist hier optional, da die Auswertung ohnehin manuell erfolgt.
Versuchsauswertung
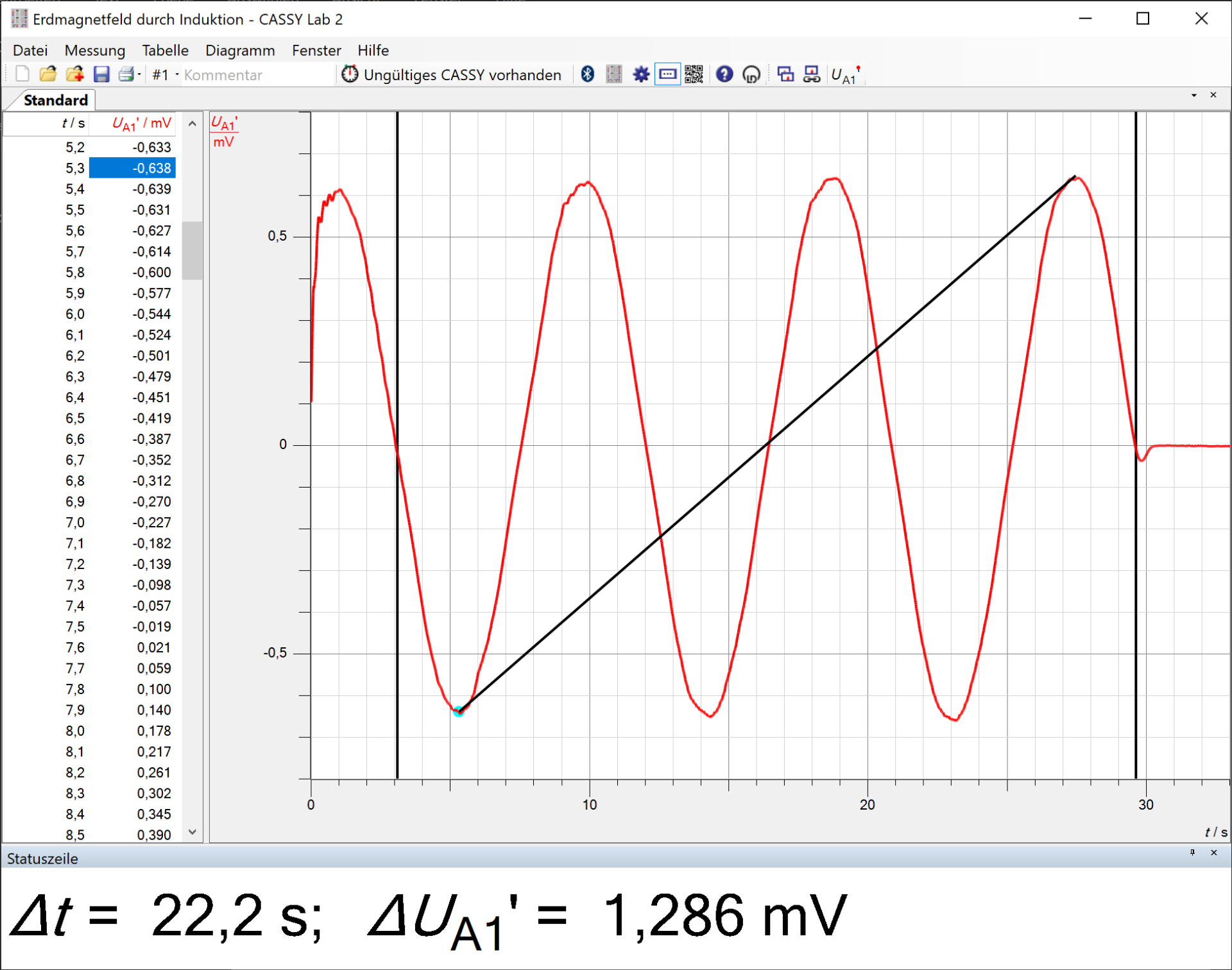
Am einfachsten und anschaulichsten ist die Auswertung, wenn die aufgenommenen Messwerte z.B. mittels USB-Kabel auf einen PC mit Cassy übertragen werden. Hier kann die Bestimmung der maximalen Induktionsspannung \(\hat{U}_{i}\) und der Umlaufdauer \(T\) manuell über eine Differenzenbildung (Markierung setzen -> Differenz messen) ermittelt werden (siehe Abb. 5). Alternativ kann die Auswertung auch über Auslesen der entsprechenden Werte in der Tabellendarstellung auf dem Mobile-Cassy erfolgen.
Im Messbeispiel ist \(\hat{U}_{i}=\frac{\Delta U_{\rm{A1}'}}{2}=0{,}643\,\rm{mV}\) und \(T=\frac{\Delta t}{2{,}5}=8{,}88\,\rm{s}\). Damit ergibt sich\[B_{\rm{h}}=\frac{0{,}643\cdot 10^{-3}\,\rm{V}\cdot {8{,}88\,\rm{s}}}{320 \cdot \pi\cdot \left(0{,}067\,\rm{m}\right)^2 \cdot 2\cdot \pi}\approx 20\,\rm{\mu T}\]
Versuchsdurchführung über Spannungsstoß
Versuchsgeräte
- Erdinduktor mit \(N = 100\) Windungen und einem Radius von \(r=13{,}8\,\rm{cm}\)
- Kompass
- Digitales Mikrovoltmeter, mit dem auch Spannungsstöße gemessen werden können
Versuchsdurchführung
Bestimmung der Horizontalkomponente
Mit Hilfe eines Kompasses bestimmt man die Nord-Süd-Richtung. Die Induktionsspule ist dann wie folgt auszurichten:
- Die Achse, um welche die Spule später gedreht wird, steht senkrecht zur Unterlage. Die Spule wird dann so gedreht, dass die Spulenebene senkrecht zur Nord-Süd-Richtung steht.
- Die Spule wird nun an der Kurbel um 90° gedreht und der entstandene Spannungsstoß am digitalen Messgerät abgelesen. Dabei ergab sich für den Spannungsstoß:\[\int_{{t_1}}^{{t_2}} {Udt} = 0{,}14 \cdot {10^{ - 3}}{\rm{Vs}}\]
Bestimmung der Horizontalkomponente
Mit Hilfe eines Kompasses bestimmt man die Nord-Süd-Richtung. Die Induktionsspule ist dann wie folgt auszurichten:
- Die Achse, um welche die Spule später gedreht wird, steht senkrecht zur Unterlage. Die Spule wird dann so gedreht, dass die Spulenebene senkrecht zur Nord-Süd-Richtung steht.
- Die Spule wird nun an der Kurbel um 90° gedreht und der entstandene Spannungsstoß am digitalen Messgerät abgelesen. Dabei ergab sich für den Spannungsstoß:\[\int_{{t_1}}^{{t_2}} {Udt} = 0{,}14 \cdot {10^{ - 3}}{\rm{Vs}}\]
Versuchsauswertung
Aus dem Messwert des jeweiligen Spannungsstoßes bestimmst du die Horizontalkomponente \(B_{\rm{h}}\) und die Vertikalkomponente \(B_{\rm{v}}\) des Erdmagnetfeldes. Ort der Messung hier war München.
Für den Zusammenhang zwischen dem Spannungsstoß und der magnetischen Flussänderung gilt\[\left| {\int_{{t_1}}^{{t_2}} {Udt} } \right| = \left| { - N \cdot \Delta \Phi } \right|\quad \left( 1 \right)\]Für die Flussänderung gilt\[\left| {\Delta \Phi } \right| = \left| { - B \cdot \Delta A} \right|\quad \Rightarrow \quad \left| {\Delta \Phi } \right| = \left| { - B \cdot \left( {0 - A} \right)} \right|\quad \Rightarrow \quad \quad \left| {\Delta \Phi } \right| = \left| {B \cdot {r^2} \cdot \pi } \right| \quad \left( 2 \right)\]Setzt man (2) in (1) ein und löst nach B auf, so erhält man\[B = \frac{{\left| {\int_{{t_1}}^{{t_2}} {Udt} } \right|}}{{\left| {N \cdot {r^2} \cdot \pi } \right|}}\]Für die Horizontalkomponente ergibt sich dann\[{B_h} = \frac{{0,14 \cdot {{10}^{ - 3}}}}{{\left| {100 \cdot {{0,138}^2} \cdot \pi } \right|}}\frac{{{\rm{Vs}}}}{{{{\rm{m}}^{\rm{2}}}}} \approx 23\,{\rm{\mu T}}\]Für die Vertikalkomponente ergibt sich dann\[{B_v} = \frac{{0,27 \cdot {{10}^{ - 3}}}}{{\left| {100 \cdot {{0,138}^2} \cdot \pi } \right|}}\frac{{{\rm{Vs}}}}{{{{\rm{m}}^{\rm{2}}}}} \approx 45\,{\rm{\mu T}}\]