Einführung
Die folgende Vorgehensweise geht auf den Lehrgang von Franz Embacher von der Uni Wien zurück. Mit einfachen Animationen können Effekte wie Längenkontraktion, Zeitdilatation und Relativität der Gleichzeitigkeit sehr anschaulich demonstriert werden.
Als physikalischen Vorgang betrachten wir eine Photonenquelle (rot), die sich im Zentrum einer kreisförmigen Anordnung befindet. Wir betrachten zwei Ereignisse:
Ereignis "Senden"
Die Quelle sendet gleichzeitig vier Photonen ("Lichtteilchen", die sich mit der Geschwindigkeit \(c = 3{,}0 \cdot {10^8}\,\frac{{\rm{m}}}{{\rm{s}}}\) bewegen) nach oben, unten, links und rechts aus. Die Photonen sind durch blaue Kugeln symbolisiert. Die Photonen werden beim Auftreffen an die Kreislinie von dort angebrachten Spiegeln reflektiert.
Ereignis "Empfangen"
Nach der Reflexion laufen die Photonen wieder zur Quelle zurück und treffen zur gleichen Zeit dort ein. Dieses Ereignis wird durch das Ticken einer Uhr verdeutlicht.
Mit Hilfe einer eingeblendeten Uhrzeit (\(1{,}00\,{\rm{ns}} = 1{,}00 \cdot {10^{ - 9}}\,{\rm{s}}\)) kann der zeitliche Verlauf der Vorgänge in dem System, das wir als Ruhesystem der Photonenquelle bezeichnen, verfolgt werden.
Aufgabe
Die Vorgänge in der Animation in Abb. 1 sind verlangsamt dargestellt. Entnimm der Animation die relevanten Daten und prüfe rechnerisch nach, ob die Photonengeschwindigkeit in der Animation der Lichtgeschwindigkeit \(c\) entspricht.
Betrachtung nach dem klassischen Relativitätsprinzip
Die Animation in Abb. 2 zeigt den in Abb. 1 vorgestellten Vorgang von einer Beobachterin (Tante Emma) aus betrachtet, die sich mit der konstanten Geschwindigkeit \(v\) gegenüber dem Ruhesystem nach links bewegt. Aus Sicht der Beobachterin bewegt sich dann das Ruhesystem mit der konstanten Geschwindigkeit \(v\) nach rechts, was wir im weiteren Verlauf unserer Überlegungen auch so darstellen werden.
In der Animation in Abb. 3 ist links nochmals der physikalische Vorgang in seinem Ruhesystem dargestellt. Rechts wird das System aus der Sicht von Tante Emma dargestellt (von Tante Emma aus gesehen bewegt sich das System nach rechts). Dabei wird von der klassischen Vorstellung der Geschwindigkeitsaddition ausgegangen, wie sie GALILEI eingeführt hat.
Widerspruch zur Konstanz der Lichtgeschwindigkeit
Damit im System von Tante Emma die Ereignisse "Senden" (alle vier Photonen werden gleichzeitig ausgesandt) und "Empfangen" (alle vier Photonen kommen gleichzeitig zurück zur Quelle) auftreten, müssen für die Photonen unterschiedliche Geschwindigkeiten angenommen werden. Das Licht müsste sich also in unterschiedliche Richtungen unterschiedlich schnell ausbreiten.
Je nach Bewegungsrichtung haben die Photonen bei dieser Betrachtung "Überlichtgeschwindigkeit" oder auch "Unterlichtgeschwindigkeit", was einen Widerspruch zu EINSTEINSs Postulat der Konstanz der Lichtgeschwindigkeit darstellt.
Aufgabe
Entnimm der Animation in Abb. 3 die relevanten Daten und bestimme damit die Relativgeschwindigkeit \(v\) zwischen dem Ruhesystem des physikalischen Vorgangs und Tante Emmas System.
Berücksichtigung des Postulates der Konstanz der Lichtgeschwindigkeit in allen Inertialsystemen
Hinweis: Der lila Kreis stellt den geometrischen Ort dar, auf dem sich die Photonen bewegen, welche zum Zeitpunkt Null von der bewegten Quelle ausgesandt wurden.
Der Versuch von MICHELSON und MORLEY zeigt, dass Licht in allen Inertialsystemen die gleiche Geschwindigkeit \(c\) besitzt. Dies wird in der Animation in Abb. 5 berücksichtigt. Als Konsequenz dieser Betrachtungsweise erkennt man aber, dass das Ereignis "Empfang" (d.h. alle vier Photonen kehren gleichzeitig zur bewegten Quelle zurück) nicht mehr auftritt. Dies ist jedoch ein Widerspruch zum Relativitätsprinzip.
Außerdem kann man der Animation entnehmen, dass die Zeitspanne \(\Delta t\), die Tante Emma beim bewegten System zwischen der Emission des nach oben laufenden Photons und der Reflexion am oberen Spiegel feststellt, größer ist als die entsprechende Zeit \(\Delta t'\) im Ruhesystem. Im gewählten Beispiel gilt \(\Delta t \approx 0{,}63\,{\rm{ns}}\) und \(\Delta t' \approx 0{,}50\,{\rm{ns}}\). Dies liegt daran, dass das im bewegten System nach schräg oben laufende Photon eine längere Strecke zum oberen Spiegel durchlaufen muss als das entsprechende Photon im Ruhesystem.
Aus dieser Betrachtung erkennt man schon ohne große Rechnung, dass die Zeit im Ruhesystem der Photonenquelle, das gegenüber Tante Emmas System bewegt ist, langsamer verläuft als für Tante Emma. Man bezeichnet diese Erscheinung die unserem gesunden Menschenverstand1 zu widersprechen scheint als Zeitdilatation. Prof. Sexl drückte dies so aus: "Zeit ist Privatsache".
1 Einstein soll gesagt haben: Der gesunde Menschenverstand ist die Summe aller unserer Vorurteile.
Zeitdilatation
Die Animation in Abb. 6 zeigt die Herleitung einer quantitativen Beziehung zwischen \(\Delta t'\) und \(\Delta t\). Sie ist für das weitere Verständnis dieses Artikels nicht nötig, wird aber später von großer Wichtigkeit sein.
Durch eine einfach geometrische Betrachtung und durch die Anwendung des Satzes von PYTHAGORAS lässt sich ein Zusammenhang zwischen Zeitspannen im Ruhesystem und bewegten System herstellen.
In der Animation ist die Aussendung eines Photons zum oberen Spiegel (Entfernung des Spiegels von der Quelle wird mit R bezeichnet) im Ruhesystem und im bewegten System noch einmal dargestellt. Dabei wird die Bahn nur kleine Spurpunkte festgehalten. Ein äußerer Beobachter stellt fest, dass das Photon im bewegten System von der Quelle bis zum Erreichen des oberen Spiegels eine größere Strecke zurückzulegen hat, als das entsprechende Photon im Ruhesystem. Aufgrund der Konstanz der Lichtgeschwindigkeit muss daher \(\Delta t' < \Delta t\) gelten.
Im Ruhesystem der Photonen (gestrichene Größen) gilt\[R = c \cdot \Delta t'\]Im System von Tante Emma (ungestrichene Größen) beträgt die vom Photon zurückgelegt Strecke\[c \cdot \Delta t\]und die vom System seit Aussendung des Photons zurückgelegte Strecke\[v \cdot \Delta t\]Durch Anwendung des Satzes von PYTHAGORAS auf das rechtwinklige Dreieck im rechten Teil der Animation erhält man\[\begin{eqnarray}{\left( {c \cdot \Delta t} \right)^2} &=& {\left( {v \cdot \Delta t} \right)^2} + {\left( {c \cdot \Delta t'} \right)^2}\\ {\left( {c \cdot \Delta t'} \right)^2} &=& {\left( {c \cdot \Delta t} \right)^2} - {\left( {v \cdot \Delta t} \right)^2}\\ \Delta {{t'}^2} &=& \Delta {t^2} \cdot \frac{{{c^2} - {v^2}}}{{{c^2}}}\\ \Delta {{t'}^2} &=& \Delta {t^2} \cdot \left( {1 - {{\left( {\frac{v}{c}} \right)}^2}} \right)\\ \Delta t' &=& \Delta t \cdot \sqrt {\left( {1 - {{\left( {\frac{v}{c}} \right)}^2}} \right)} \end{eqnarray}\]Wendet man diesen Zusammenhang auf das Beispiel in der Animation an, so erhält man\[\Delta t' = 0{,}63\,{\rm{ns}} \cdot \sqrt {\left( {1 - {{\left( {\frac{{0{,}6 \cdot c}}{c}} \right)}^2}} \right)} = 0{,}63\,{\rm{ns}} \cdot \sqrt {1 - {{0{,}36}^2}} = 0{,}63\,{\rm{ns}} \cdot 0{,}8 \approx 0{,}5\,{\rm{ns}}\]Diese Zeitspanne ist auch an der Uhr im Ruhesystem der Photonen abzulesen.
Längenkontraktion
Hinweis: Der lila Kreis stellt den geometrischen Ort dar, auf dem sich die Photonen bewegen, welche zum Zeitpunkt Null von der bewegten Quelle ausgesandt wurden.
Unter der Überschrift "Berücksichtigung der Konstanz der Lichtgeschwindigkeit in allen Inertialsystemen" kamen die horizontal laufenden Photonen im Vergleich zu den vertikal laufenden Photonen stets verspätet im Zentrum an, damit das Ereignis "Empfang" eintreten konnte. EINSTEIN löste diesen Widerspruch durch die Annahme auf, dass Längen in Bewegungsrichtung verkürzt sind, d.h. die Längen bewegter Gegenstände werden vom System Tante Emmas kürzer gemessen als im Ruhesystem (Längenkontraktion). Für die Animation in Abb. 7 bedeutet dies, dass die Linie an der die Photonen reflektiert werden, kein Kreis sondern eine Ellipse ist.
Deutung des Gedankenexperimentes mit Hilfe von EINSTEIN
Mit dieser Verkürzung der Längen in Bewegungsrichtung werden die in den Animationen in Abb. 3 und Abb. 5 beobachteten Widersprüche beseitigt. Die Photonen gelangen nach Reflexion an den Wänden der Ellipse gleichzeitig wieder zur Quelle, d.h. das Ereignis "Empfang" ist wieder festzustellen und das unter Berücksichtigung der Konstanz der Lichtgeschwindigkeit. Allerdings ist der Zeitabstand zwischen zwei aufeinanderfolgenden Ereignissen "Empfang" im bewegten System ein anderer als im Ruhesystem (dies soll ihnen das Klicken im jeweiligen System verdeutlichen). Die Zeitdauer zwischen zwei benachbarten Ereignissen "Empfang" bei dem dargestellten Beispiel ist im Ruhesystem der Photonenquelle \(1{,}0\,\rm{ns}\), im System von Tante Emma aber \(1{,}25\,\rm{ns}\). Diese führt zu der Aussage
Zeitdilatation
Eine bewegte Uhr geht langsamer als eine gleichartige im Ruhesystem! (Zeitdilatation)
Zwischen der vergangenen Zeit \(\Delta t'\) im mit der Geschwindigkeit \(v\) bewegten Bezugssystem und der Zeit \(\Delta t\) im Ruhesystem gilt die Beziehung\[\Delta t'=\Delta t \cdot \sqrt{{1 - {{\left( \frac{v}{c} \right)}^2}}}\]
Darüber hinaus erkennt man in der Animation auch noch: Die Reflexion der horizontal laufenden Photonen an der Wand geschieht im Ruhesystem der Photonenquelle gleichzeitig, im Bezugssystem von Tante Emma finden diese Reflexionen zu verschiedenen Zeiten statt. Gleichzeitigkeit hängt also davon ab, von welchem Bezugssystem aus die Beobachtung erfolgt: Man spricht von der Relativität der Gleichzeitigkeit.
Damit die beiden EINSTEINschen Postulate zur speziellen Relativitätstheorie erfüllt werden konnten, musste im System von Tante Emma der Kreis zu einer Ellipse "zusammengedrückt" werden. Der Verkürzungsfaktor in Querrichtung beträgt allgemein\[\sqrt {1 - {{\left( {\frac{v}{c}} \right)}^2}} \]
Denkt man sich in Querrichtung in das Ruhesystem und das bewegte System einen Maßstab gelegt, so gilt zwischen deren Längen die folgende Beziehung:
Längenkontraktion
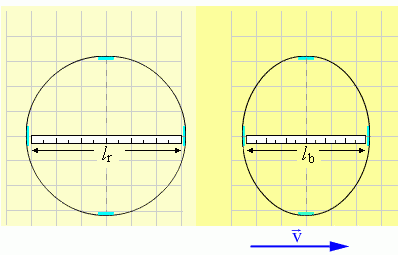
Ein bewegter Maßstab ist in Bewegungsrichtung kürzer als im Ruhesystem! (Längenkontraktion)
Zwischen der Länge im mit der Geschwindigkeit \(v\) bewegten Bezugssystem \({l_b}\) und der Länge im Ruhesystem \({l_r}\) gilt die Beziehung \[{l_b} = {l_r} \cdot \sqrt {1 - {{\left( {\frac{v}{c}} \right)}^2}} \]