|
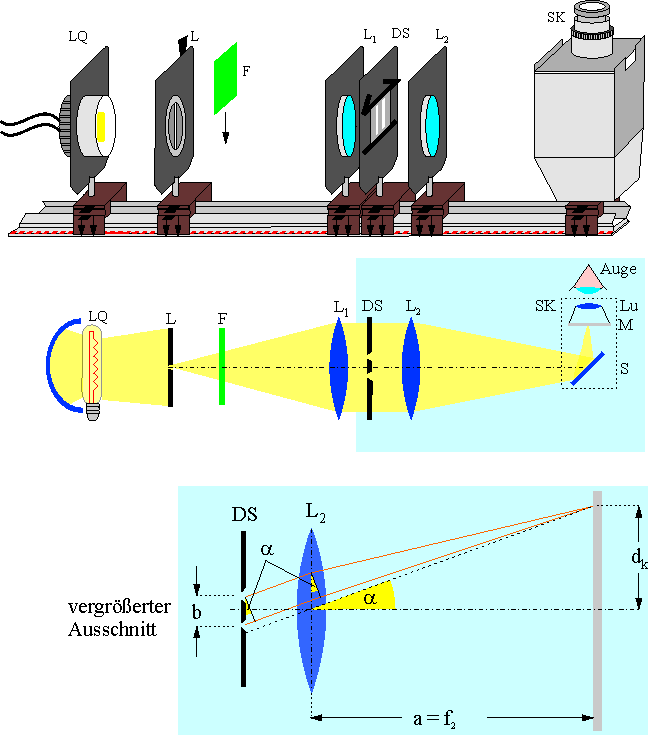
Der Einfachspalt L wird mit einer Halogenlampe beleuchtet. Der Einfachspalt steht in der Brennebene der Linse L1, so dass das vom Spalt L ausgehende divergente Lichtbündel zu einem Parallelbündel gewandelt wird. Das Parallelbündel wird durch die Linse L2 scharf auf die Mattscheibe M des Spiegelkastens abgebildet. Das Auge betrachtet diese Mattscheibe mit Hilfe einer kleinen Lupe Lu. Mattscheibe, Lupe und Umlenkspiegel S befinden sich im sogenannten Spiegelkasten SK. Bringt man nun den Doppelspalt DS in das Parallelbündel zwischen den beiden Linsen, so erfolgt die Beugung des Lichts. Auf der Mattscheibe sind sehr gut die Interferenzerscheinungen, die durch den Doppelspalt hervorgerufen werden (subjektiv) zu beobachten. Mit Hilfe des Farbfilters F kann eine Farbauswahl getroffen werden. |
 |
Teilversuch 1
Variation des Spaltmittenabstands b
bei gleicher Spaltbreite B
Teilversuch 2
Variation der Spaltbreite B
bei gleichem Spaltmittenabstand b
Teilversuch 3
Variation der Lichtfarbe
bei gleichem b und B

Für das k-te Maximum gilt
\[ \Delta s = k \cdot \lambda \]
Außerdem gilt (vgl. Skizze)
\[ \Delta s = b \cdot \sin{\alpha_k} \Rightarrow k \cdot \lambda = b \cdot \sin{\alpha_k} \Rightarrow \lambda = \frac{b \cdot \sin{\alpha_k}}{k} \text{ (1) } \]
Da sich alle Parallelstrahlen in der Brennebene an dem Ort treffen, wo auch der Hauptstrahl (Strahl durch das Linsenzentrum) den Schirm treffen würde, gilt (wobei f2 die Brennweite der Linse L2 ist):
\[ \tan{\alpha_k} = \frac{d_k}{f_2} \text{ (2) } \]
Mit der Kleinwinkelnäherung \( \sin{\alpha} = \tan{\alpha} \) folgt mit (1) und (2)
\[ \lambda = \frac{b \cdot d_k}{k \cdot f_2} \]
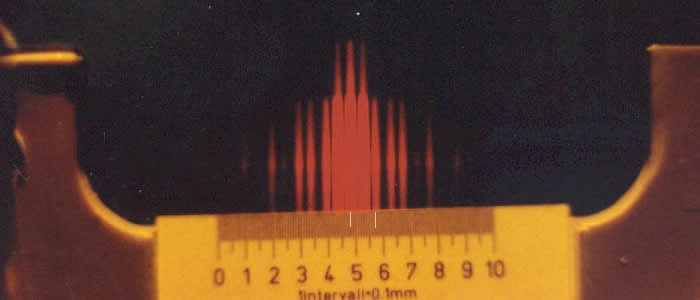
Die Linse 2 hatte eine Brennweite von f2 = 297 mm. Die Auswertung erfolgt mit Hilfe des Maximums 2. Ordnung anhand der Bilder bei der Variation der Lichtfarbe (beachten Sie hier die kleinen weißen Markierungen beim 0. und beim 2. Maximum):
|
Für blaues Licht ergab sich für d2 = 0,50 mm: |
|
Für grünes Licht ergab sich für d2 = 0,70 mm: |
|
Für rotes Licht ergab sich für d2 = 0,50 mm: |