a) Nur bei den beiden skizzierten Strahlen 1 und 2 ist der Gangunterschied so klein, dass die Kohärenzbedingung erfüllt werden kann ("Normales" Licht hat eine relativ kurze Kohärenzlänge. Ist der Gangunterschied zu groß, so kommt es aufgrund der unterschiedlichen Laufzeiten nicht zur Überlappung der beiden Wellenzüge auf einem Schirm zu einem bestimmten Zeitpunkt).
Der Gangunterschied zwischen zwei Strahlen, die z.B. jeweils an der Unterseite der Glasplatten reflektiert werden, ist in der Regel schon zu groß.
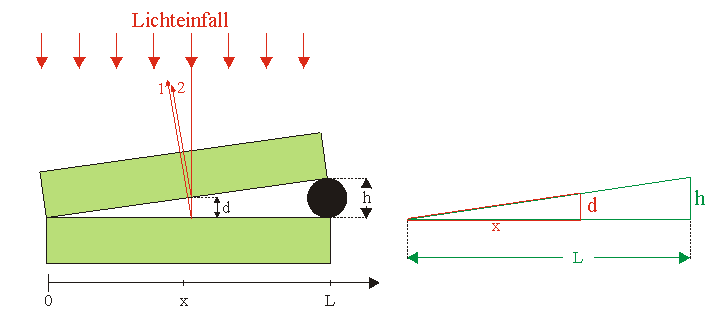
b) Berechnung des Gangunterschiedes (Berücksichtigung des Phasensprungs bei Reflexion von Strahl 1): \[\Delta s = 2 \cdot {d_k} + \frac{\lambda }{2}\quad(1)\] Ausdrücken von dk durch \(h\), \(L\) und \(x_k\) (Strahlensatz):< \[\frac{{{d_k}}}{h} = \frac{{{x_k}}}{L} \Leftrightarrow {d_k} = h \cdot \frac{{{x_k}}}{L}\quad(2)\] Einsetzen von \((2)\) in \((1)\) liefert \[\Delta s = 2 \cdot h \cdot \frac{{{x_k}}}{L} + \frac{\lambda }{2}\] Für das \(k\)-te Maximum gilt< \[\Delta s = k \cdot \lambda \] Somit ergibt sich für \(x_k\) \[k \cdot \lambda = 2 \cdot h \cdot \frac{{{x_k}}}{L} + \frac{\lambda }{2} \Leftrightarrow L \cdot \lambda \cdot \left( {k - \frac{1}{2}} \right) = 2 \cdot h \cdot {x_k} \Leftrightarrow {x_k} = \frac{{L \cdot \lambda \cdot \left( {k - \frac{1}{2}} \right)}}{{2 \cdot h}}\] und analog für \(x_{k+1}\) \[{x_{k + 1}} = \frac{{L \cdot \lambda \cdot \left( {k + \frac{1}{2}} \right)}}{{2 \cdot h}}\] Somit folgt für den Abstand benachbarter Maxima \[\Delta x = {x_{k + 1}} - {x_k} = \frac{{L \cdot \lambda \cdot \left( {k + \frac{1}{2}} \right)}}{{2 \cdot h}} - \frac{{L \cdot \lambda \cdot \left( {k - \frac{1}{2}} \right)}}{{2 \cdot h}} = \frac{{L \cdot \lambda }}{{2 \cdot h}}\] Aus der Folge der Interferenzstreifen kann man sehen \[\Delta x = \frac{a}{5} \Rightarrow \Delta x = \frac{{1,50 \cdot {{10}^{ - 2}}{\rm{m}}}}{5} = 0,30 \cdot {10^{ - 2}}{\rm{m}}\] Somit ergibt sich für \(h\) \[\Delta x = \frac{{L \cdot \lambda }}{{2 \cdot h}} \Leftrightarrow h = \frac{{L \cdot \lambda }}{{2 \cdot \Delta x}} \Rightarrow h = \frac{{0,10{\rm{m}} \cdot 600 \cdot {{10}^{ - 9}}{\rm{m}}}}{{2 \cdot 0,30 \cdot {{10}^{ - 2}}{\rm{m}}}} = 1,0 \cdot {10^{ - 5}}{\rm{m}} = \frac{1}{{100}}{\rm{mm}}\]