Beim Drehen einer Schraube mit einem Schraubenschlüssel wird die Kraft, die du aufbringst über den sog. Hebelarm, also den Schraubenschlüsselgriff auf die Schraube übertragen und versetzt diese in Drehung. Je weiter außen am Schraubenschlüssel du angreifst, desto geringer ist die Kraft, die du zum Festziehen oder Lösen der Schraube aufbringen musst. Auch ein möglichst senkrechtes Ansetzen der Kraft am Schraubenschlüssel reduziert den Kraftaufwand.
Physikalisch ausgedrückt erzeugen Kraft und Schraubenschlüssel ein sog. Drehmoment \(M\). Da hier sowohl bei der Kraft als auch beim Schraubenschlüssel, neben der Größe bzw. Länge auf die Richtung eine wichtige Rolle spielt, sind sowohl die Kraft \(\vec F\) also auch der Radiusvektor \(\vec r\) des Schraubenschlüssels Vektoren.
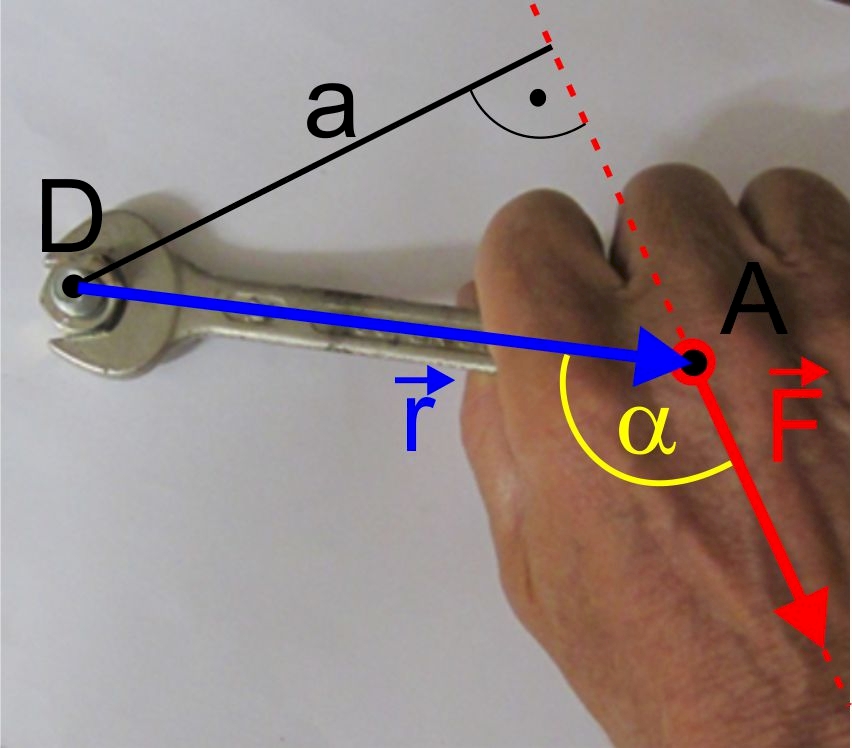
Drehmoment \(M\) und Hebelarm \(a\)
Aber auch ohne Verwendung von Vektoren kannst du das Drehmoment \(M\) berechnen: Das Drehmoment \(M\) ergibt sich aus dem Produkt des Hebelarms \(a\) und dem Betrag der Kraft \(F\):\[M = a \cdot F\]Dabei ist der Hebelarm \(a\) der Abstand des Drehpunkts von der Wirkungslinie der Kraft (siehe Abb. 1). Diesen Abstand \(a\) kannst du mittels der trigonometrischen Beziehung \(a = r \cdot \sin \left( \alpha \right) \) aus der Entfernung vom Kraft-Ansatzpunkt A zum Drehpunkt D, also dem Radiusvektor \(\vec r\), und der Winkelweite \(\alpha \) des Winkels zwischen Kraftvektor \(\vec F\) und Radiusvektor \(\vec r\) ohne weitere Verwendung des Vektorbegriff berechnen. Somit gilt\[M = r \cdot F \cdot \sin \left( \alpha \right) \]
Hinweis: In der Abbildung rechts ist die Winkelweite \(\alpha \) größer als \({90^\circ }\). Deshalb ergibt die Berechnung der Streckenlänge \(a\) hier eigentlich \(a = r \cdot \sin \left( 180^\circ - \alpha \right) \). Da aber stets \(\sin \left( {180^\circ - \alpha } \right) = \sin \left( \alpha \right)\) gilt, führt auch hier die oben angegebene Berechnungsmethode \(a = r \cdot \sin \left( \alpha \right) \) zum richtigen Ergebnis.
Richtung des Drehmoments
Was allerdings bei dieser Berechnung angenommen wird, ist die Kenntnis der Achsenrichtung und die Orientierung des Drehmoments als rechtsdrehend oder linksdrehend. Das Drehmoment ist also, da es eine Richtung und eine Orientierung hat ebenfalls ein Vektor. Dabei steht der Drehmomentvektor \(\vec M \) senkrecht auf der durch die Vektoren \(\vec r \) und \(\vec F \) aufgespannten Ebene und entspricht der Richtung der Drehachse. Die Berechnung dieses Vektors geht am einfachsten über das sogenannte Vektorprodukt (Kreuzprodukt):\[\vec M = \vec r \times \vec F \]
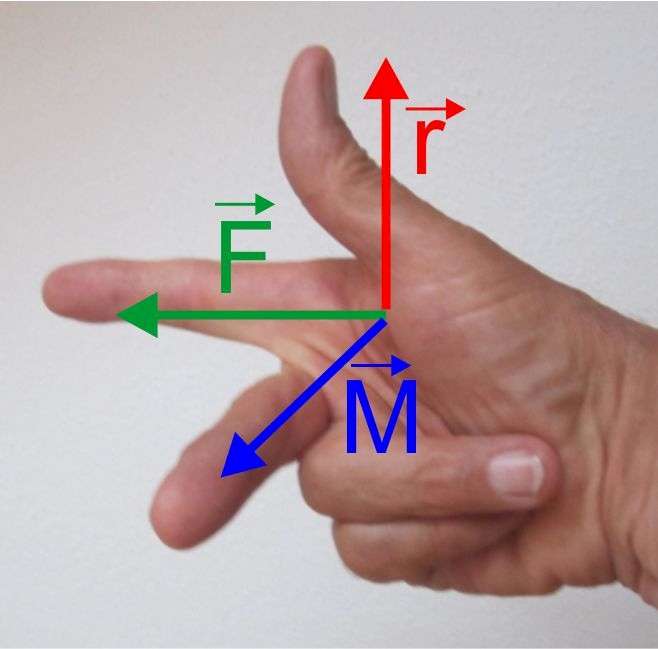
Drei-Finger-Regel der rechten Hand
Die Orientierung des Vektors kannst du aber auch einfach mit der 3-Finger-Regel der rechten Hand bestimmen: Daumen in Richtung des Radiusvektors \(\vec r \) und Zeigefinger in etwa in Richtung der Kraft \(\vec F \), dann zeigt der zu den anderen beiden Fingern senkrecht stehende Mittelfinger in Richtung des Drehmomentes \(\vec M \) an (vgl. Abb.2).
Hinweis: Der Radiusvektor und der Kraftvektor stehen oft nicht senkrecht aufeinander, aber eine grobe Ausrichtung der Finger ist ausreichend, um die Richtung des Drehmoments zu bestimmen.
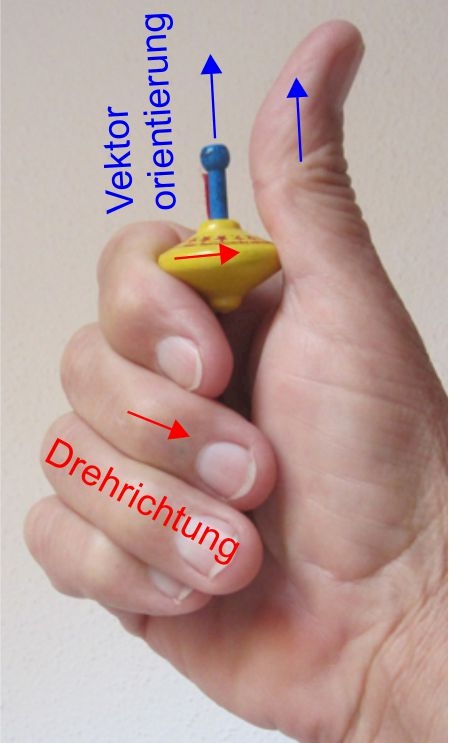
Orientierung des Drehmomentvektors mit der rechten Faust Regel
Man kann die Richtung des Drehmomentvektors aber auch mit Hilfe der Faustregel der rechten Hand herausbekommen: Zeigen die Finger der rechten Hand die Richtung an, in der sich der Körper drehen würde, so zeigt der Daumen die Orientierung des Drehmomentvektors an (siehe Abb. 3).
Die Größe dieses Vektors ist \(M = r \cdot F \cdot \sin \left(180° - \alpha \right)\).
Beispiele
Bei einer Wippe spielt das Drehmoment eine wichtige Rolle. Die beiden Personen auf den unterschiedlichen Seiten des Drehpunktes sorgen jeweils für unterschiedlich gerichtete Drehmomente - eines linksdrehend, das andere rechtsdrehend. Das größere der beiden Drehmomente bestimmt, in welche Richtung die Wippe kippt.
Ein solches Drehmoment kann aber auch wie in Abb. 4 durch eine Spiralfeder erzeugt werden. So erzeugt die Rückholfeder eines Stahlmaßbandes ein Drehmoment, sodass sich das Maßband aufwickelt.