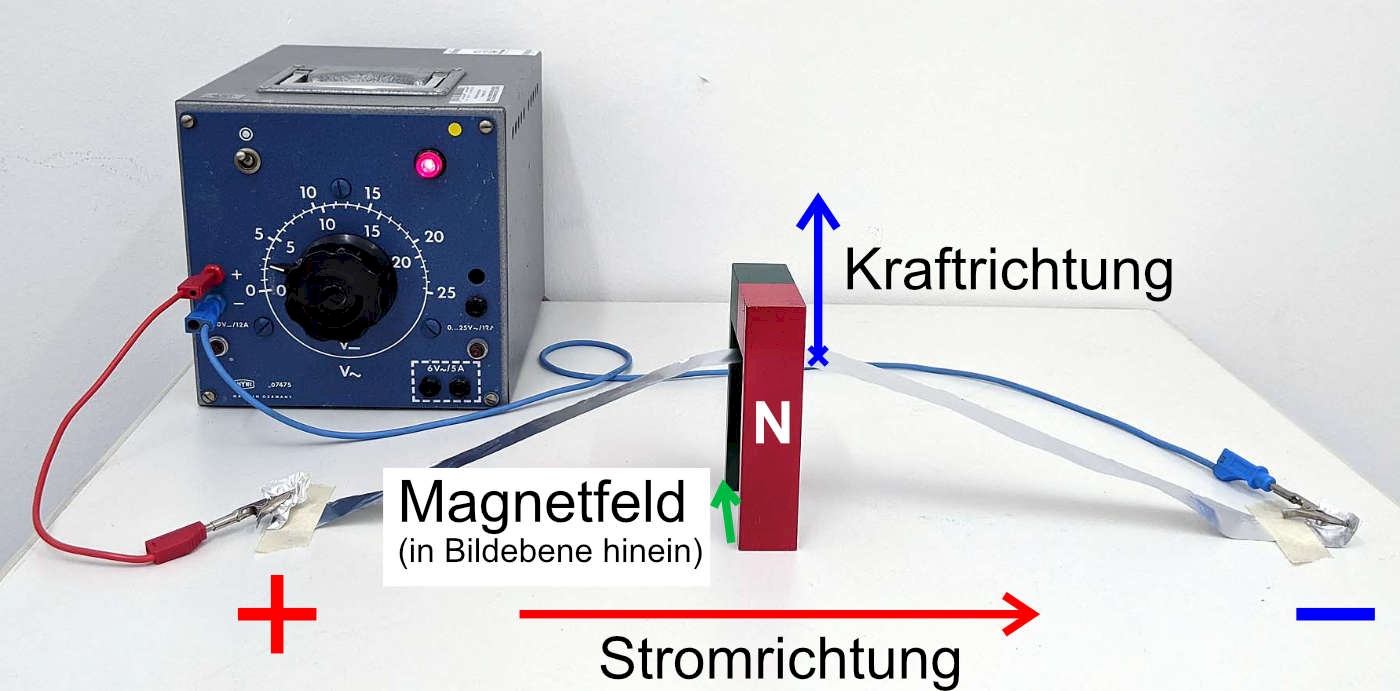
Befindet sich ein stromdurchflossener Leiter im Magnetfeld, so erfährt der Leiter im allgemeinen eine Kraft. Diese sorgt z.B. in Abb. 1 dafür, dass die stromdurchflossene Aluminiumfolie angehoben wird.
Die Wirkung dieser Kraft ist am größten, wenn Stromrichtung und Magnetfeldrichtung senkrecht zueinander stehen, also einen Winkel von \(90^\circ \) bilden. Wenn Stromrichtung und Magnetfeldrichtung hingegen parallel oder antiparallel verlaufen, wirkt keine Kraft.
Im Fall von senkrecht zueinander stehender Stromrichtung und Magnetfeldrichtung steht die wirkende Kraft senkrecht auf der durch die Stromrichtung und der Magnetfeldrichtung aufgespannten Ebene.
Drei-Finger-Regel der rechten Hand
Zur Ermittlung der Kraftrichtung kannst du drei Finger der rechten Hand und die Drei-Finger-Regel der rechten Hand verwenden (siehe Abb. 2):
- Der Daumen der rechten Hand zeigt in die Stromrichtung (von + nach -).
- Der Zeigefinger der rechten Hand zeigt in die Magnetfeldrichtung (von Nord nach Süd).
- Der Mittelfinger der rechten Hand gibt die Kraftrichtung an.
Gelegentlich wird die Drei-Finger-Regel auch als UVW-Regel (Ursache-Vermittlung-Wirkung-Regel) bezeichnet. Der Daumen zeigt in Richtung der Ursache, der Zeigefinger in Richtung des Vermittlers und der Mittelfinger in Richtung der Wirkung. Hier ist das Phänomen der Strom, das Magnetfeld der Vermittler und die Kraft die Wirkung. Um Verwirrungen mit Blick auf die Ursache (Strom bzw. Magnetfeld) zu vermeiden, nutzen wir die Bezeichnung Drei-Finger-Regel der rechten Hand.
Stromrichtung senkrecht zur Magnetfeldrichtung
Die Animationen in den Abb. 3 und 4 zeigen die Richtung der Kraft bei verschiedenen Stromrichtungen. Würde man bei den Versuchen jeweils die Magnetfeldrichtung umkehren, so würde sich auch die Richtung der Kraft auf den beweglichen Leiter umkehren. In Abb. 3 würde sich dann der Leiter nach rechts, in Abb. 4 nach links bewegen.
Stromrichtung parallel oder antiparallel zur Magnetfeldrichtung
Die Animation in Abb. 5 zeigt, dass keine Kraftwirkung auftritt, wenn Stromrichtung und Magnetfeldrichtung parallel bzw. antiparallel zueinander verlaufen.
Stromrichtung schräg zur Magnetfeldrichtung (nur für Experten)
Bilden Stromrichtung und Magnetfeldrichtung einen Winkel der Weite \(0<\varphi <90^\circ\), so wirkt auf den Leiter zwar weiterhin eine Kraft, ihr Betrag ist allerdings kleiner als im Fall, in dem Stromrichtung und Magnetfeldrichtung senkrecht zueinander stehen.
Für den Betrag der magnetischen Kraft gilt allgemein\[{F_{\rm{mag}}} = B \cdot {I_{\rm{L}}} \cdot l \cdot \sin \left( \varphi \right)\]Für \(\varphi = 90^\circ \) (Stromrichtung senkrecht zur Magnetfeldrichtung) erhält man wegen \(\sin \left( {90^\circ } \right) = 1\)\[{F_{\rm{mag}}} = B \cdot {I_{\rm{L}}} \cdot l \]Für \(\varphi = 0^\circ \) (Stromrichtung parallel/antiparallel zur Magnetfeldrichtung) erhält man wegen \(\sin \left( {0^\circ } \right) = 0\)\[{F_{\rm{mag}}} = 0 \]Du siehst also, dass die obige Formel auch die oben skizzierten Sonderfälle richtig beschreibt.
Hinweis: Durch den Versuch mit der Stromwaage wurde zunächst nur der Betrag der Stärke des Magnetfeldes \(B\) eingeführt. War der stromdurchflossene Leiter senkrecht zum Magnetfeld orientiert, so galt\[B = \frac{{{F_{mag}}}}{{{I_L} \cdot l}}\quad \quad \left[ B \right] = 1\frac{{\rm{N}}}{{{\rm{A}} \cdot {\rm{m}}}} = 1\frac{{{\rm{N}} \cdot {\rm{m}}}}{{{\rm{A}} \cdot {{\rm{m}}^2}}} = 1\frac{{\rm{J}}}{{{\rm{A}} \cdot {{\rm{m}}^2}}} = 1\frac{{{\rm{V}} \cdot {\rm{A}} \cdot {\rm{s}}}}{{{\rm{A}} \cdot {{\rm{m}}^2}}} = 1\frac{{{\rm{V}} \cdot {\rm{s}}}}{{{{\rm{m}}^2}}} = 1\,{\rm{T(Tesla)}}\]Für allgemeinere Betrachtungen geht man jedoch vom Vektor des Magnetfeldstärke \(\vec B\) aus. Die Richtung von \(\vec B\) ist durch die Richtung der magnetischen Feldlinien festgelegt.