Liegt ein Doppelsternsystem mit nahe zusammenliegenden Sternen so, dass der Beobachter auf der Erde genau in der Bahnebene liegt, so verdecken sich die Sterne in periodischen Abständen gegenseitig. Die Animation in Abb. 1 von Stanlekub [Public domain], via Wikimedia Commons zeigt diese Bewegung. Einmal ist der hellere Stern mit der größeren Oberflächentemperatur (in der Animation rechts der blaue Stern) vor dem dunkleren (in der Animation rechts der rote Stern), dann reduziert sich das Licht nur etwas, einmal ist der dunklere Stern vor dem helleren, dann reduziert sich das Licht stärker.
Aus diesen periodischen Helligkeitsschwankungen können neben der Umlaufzeit auch die Sterndurchmesser bestimmt werden. Dies erfordert allerdings sehr genaue Helligkeitsmessungen, um die nur sehr geringen Helligkeitsunterschiede beobachten zu können.
Die Bahngeschwindigkeiten \({v_{\rm{A}}}\) und \({v_{\rm{B}}}\) der beiden Sterne erhält man mit spektroskopischen Methoden aus der Dopplerverschiebung, wenn sich die Sterne auf den Beobachter zu- oder wegbewegen. Dies geht hier wegen der Lage des Beobachters in der Bahnebene sehr genau.
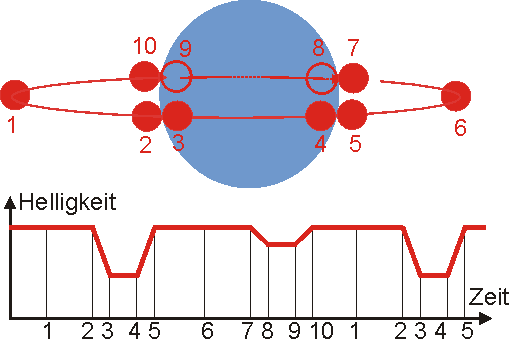
Die Sterndurchmesser \(d_{\rm{A}}\) und \(d_{\rm{B}}\) bestimmt man dagegen indirekt, wenn sich die beiden Sterne mit der Relativgeschwindigkeit \(v = {v_{\rm{A}}} + {v_{\rm{B}}}\) scheinbar aufeinander zu- bzw. voneinander wegbewegen. Bei Beachtung der nebenstehenden Abbildung gilt dann\[{d_{\rm{A}}} + {d_{\rm{B}}} = v \cdot \left( {{t_5} - {t_2}} \right)\]sowie\[{d_{\rm{A}}} - {d_{\rm{B}}} = v \cdot \left( {{t_4} - {t_3}} \right)\]woraus sich dann leicht (Lineares Gleichungssystem für \(d_{\rm{A}}\) und \(d_{\rm{B}}\)) die beiden Durchmesser zu\[{d_{\rm{A}}} = \frac{{v \cdot \left( {{t_5} - {t_2} + {t_4} - {t_3}} \right)}}{2}\]und\[{d_{\rm{B}}} = \frac{{v \cdot \left( {{t_5} - {t_2} - {t_4} + {t_3}} \right)}}{2}\]berechnen lassen.

