Gehen wir zunächst von einer Kreisbahn um die Erde aus, die in 800 km von der Eroberfläche entfernt ist, so ist der Bahnradius r der Sonde r = 6368 km + 800 km = 7168 km = 7,168·106 m.
Bahngeschwindigkeit
Auf der Kreisbahn der Sonde ist die Gravitationskraft die Zentripetalkraft, woraus man die Bahngeschwindigkeit bestimmt
\[m \cdot \frac{{{v^2}}}{r} = G \cdot \frac{{m \cdot M}}{{{r^2}}} \Rightarrow v = \sqrt {G \cdot \frac{M}{r}} \]
Einsetzen der gegebenen Werte liefert
\[v = \sqrt {6,67 \cdot {{10}^{ - 11}}{\mkern 1mu} \frac{{{{\rm{m}}^{\rm{3}}}}}{{{\rm{kg}} \cdot {{\rm{s}}^{\rm{2}}}}} \cdot \frac{{5,977 \cdot {{10}^{24}}{\rm{kg}}}}{{7,168 \cdot {{10}^6}{\rm{m}}}}} = 7,46 \cdot {10^3}\frac{{\rm{m}}}{{\rm{s}}}\]
Bei dieser Umlaufgeschwindigkeit (22 fache Schallgeschwindigkeit) dauert eine Erdumkreisung 6000 s = 1 h 40 min.
Energie im Gravitationsfeld
- Die potentielle Energie eines Massekörpers der Masse m im Gravitationsfeld der Erde mit der Masse M gegenüber dem unendlich fernen Punkt ist \({E_{{\rm{pot}}}} = - G \cdot \frac{{m \cdot M}}{r}\), wobei r der Abstand der Massenmittelpunkte ist.
- Die kinetische Energie auf der Kreisbahn ist \({E_{{\rm{kin}}}} = \frac{1}{2} \cdot m \cdot {v^2} = \frac{1}{2} \cdot G \cdot \frac{{m \cdot M}}{a}\), also die Hälfte des Betrags der potentiellen Energie.
- Die Gesamtenergie als Summe von potentieller und kinetischer Energie ist gegenüber dem unendlichen negativ und vom Betrag gleich der kinetischen Energie auf der Kreisbahn, bzw. der halben potentiellen Energie.
Energiezuwachs durch das Sonnensegel
Will man die Zeit bis zum Verlassen der Sonde aus dem der Erdanziehungsbereich abzuschätzen, scheint der folgende Ansatz zunächst plausibel:
Beschleunigung auf die Fluchtgeschwindigkeit
Man beschleunigt die Sonde durch das Sonnensegel auf die Größe der Fluchtgeschwindigkeit aus der Umlaufbahn. Das würde bedeuten, dass man die vorhandene kinetische Energie verdoppeln müsste, also die Geschwindigkeit mit \(\sqrt 2 \) multiplizieren.
=> v1 = 7,46·103 m/s und v2 = 10,55·103 m/s , damit ergibt sich ein Geschwindigkeitsunterschied von Δv = 3,09·103 m/s.
Dieser Geschwindigkeitsunterschied wird durch eine Beschleunigung erreicht, die im Maximum
amax = 5,4·10-5 m/s2 beträgt und im zeitlichen Mittel auf der Kreisbahn die Hälfte davon ist (Herleitung siehe Kasten).
\(\bar a = \frac{{\Delta v}}{{\Delta t}} \Leftrightarrow \Delta t = \frac{{\Delta v}}{{\bar a}} \Rightarrow \Delta t = \frac{{3090\frac{{\rm{m}}}{{\rm{s}}}}}{{2,7 \cdot {{10}^{ - 5}}\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}}} = 1,14 \cdot {10^8}{\rm{s}} = 3,6{\rm{a}}\)
|
Herleitung für Interessierte
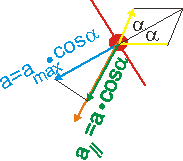
Bei optimalem Einstellwinkel α der Segelnormale zum eintreffen Licht ist der
Beschleunigungsbetrag a = amax·cos α ,
und die Beschleunigungskomponente in Bewegungsrichtung a// = a·cos α = amax·(cos α)2
Die mittlere Beschleunigung ist dann
\[\bar a = \frac{1}{{0,5\pi }} \cdot {a_{{\rm{max}}}} \cdot \int\limits_0^{0,5\pi } {\cos {{\left( \alpha \right)}^2}} d\alpha = \frac{1}{{0,5\pi }} \cdot {a_{{\rm{max}}}} \cdot \left[ {\frac{1}{2} \cdot \left( {\alpha + \sin \left( \alpha \right) \cdot \cos \left( \alpha \right)} \right)} \right]_0^{0,5\pi } = 0,5 \cdot {a_{{\rm{max}}}}\]
|
 |
Dieser Ansatz, der stets von optimalem Vortrien ausgeht, berücksichtigt in keiner Weise, dass die Sonde durch die Energiezufuhr auf eine höhere Bahn gelangt und dabei Stück für Stück immer wieder Geschwindigkeit verliert, andererseits aber die Fluchtgeschwindigkeit von diesen höheren Bahnen geringer ist.
Energiegewinn bei einem Umlauf
Ein anderer Ansatz ist es, den Energiegewinn der Sonde bei einem Umlauf zu berechnen.
Auf einem Umlauf ist die mechanische Arbeit an der Sonde \({W_{{\rm{mech}}}} = \vec F \cdot \vec s\).
Die mittlere Kraft ist 0,5·amax·m, der Weg ist 2rπ. Daraus folgt:
WMech= 2,7·10-5 m/s2·100kg·2·7,168·106·3,14 m = 123 kJ
Die notwendige Energiezunahme zum Verlassen der Erdanziehung ist:
\[ - {E_{{\rm{ges}}}} = \frac{1}{2} \cdot G \cdot \frac{{m \cdot M}}{r} \Rightarrow - {E_{{\rm{ges}}}} = \frac{1}{2} \cdot 6,67 \cdot {10^{ - 11}}{\mkern 1mu} \frac{{{{\rm{m}}^{\rm{3}}}}}{{{\rm{kg}} \cdot {{\rm{s}}^{\rm{2}}}}} \cdot \frac{{100{\rm{kg}} \cdot 5,977 \cdot {{10}^{24}}{\rm{kg}}}}{{7,168 \cdot {{10}^6}{\rm{m}}}} = 2,78 \cdot {10^9}{\rm{J}}\]
Man bräuchte 2,78·109 J : 1,23·105 J = 23 000 solche Erdumkreisungen zum Verlassen der Erdanziehung.
Eine Erdumkreisungen dauert 1h 40 min. Würde man dies hochrechnen, ergäbe sich auch hier eine Zeit von 3,6 Jahren um die Sonde aus dem Erdanziehungsbereich zu entfernen. Diese Berechnung ist mit dem selben Fehler behaftet ist, dass die Sonde mit wachsender Gesamtenergie sich auf größer werdenden und längere Zeit in Anspruch nehmenden Kreisen um die Erde bewegt.
Die Bahnänderung in einem Monat
Der Ansatz ist aber geeignet um die Größe der Umlaufbahn nach einem Monat abzuschätzen.
In einem Monat erfolgen (30·24):1,67 = 431 solche Umdrehungen und die Gesamtenergie der Sonne nimmt, stets das Optimum vorausgesetzt 431· 123 kJ = 53 MJ Energie zusätzlich auf.
Ihre Gesamtenergie ist demnach:
- 2,78·109 J + 0,053·109 J = - 2,73·109 J
Daraus kann man den Bahnradius berechnen:
\[{E_{{\rm{ges}}}} = - \frac{1}{2} \cdot G \cdot \frac{{m \cdot M}}{r} \Leftrightarrow r = - \frac{1}{2} \cdot G \cdot \frac{{m \cdot M}}{{{E_{{\rm{ges}}}}}}\]
Einsetzen der gegebenen Werte liefert
\[r = \frac{1}{2} \cdot 6,67 \cdot {10^{ - 11}}{\mkern 1mu} \frac{{{{\rm{m}}^{\rm{3}}}}}{{{\rm{kg}} \cdot {{\rm{s}}^{\rm{2}}}}} \cdot \frac{{100{\rm{kg}} \cdot 5,977 \cdot {{10}^{24}}{\rm{kg}}}}{{2,78 \cdot {{10}^9}{\rm{J}}}} = 7,305 \cdot {10^6}{\rm{m}}\]
7305 km - 6368 km = 937 km.
Die Sonde hat sich in einem Monat von 800 km auf 937 km von der Erdoberfläche entfernt.




