Um Naturphänomene oder andere komplexe physikalische Erscheinungen besser erklären zu können, verwenden Naturwissenschaftler häufig sog. Modelle.
Dabei ist hier mit Modell häufig nicht ein verkleinertes Abbild des zu untersuchenden Objektes (wie z.B. die Modelleisenbahn ein verkleinertes, möglichst naturgetreues Abbild der realen Eisenbahn ist) gemeint, sondern an eine vereinfachte, anschauliche Vorstellung vom - meist komplizierten - zu untersuchenden Objekt.
Theoretische und gegenständliche Modelle
Oft ist diese Vorstellung rein gedanklicher Natur, sodass man von einem theoretischen Modell spricht. Lichtstrahlen, Magnetpole, Feldlinien und Massepunkte sind solche theoretischen Modelle. Auch das Teilchenmodell für Festkörper, Flüssigkeiten und Gase kann als theoretisches Modell angesehen werden. Es gibt aber auch gegenständliche Modelle, wie bspw. Motorenmodelle, Globen oder mit Federn verbundene Modelle von Kristallen. Diese gegenständlichen Modelle müssen dabei nicht immer dreidimensional und anfassbar sein. Auch Bilder und symbolische Darstellungen, wie bspw. Schaltskizzen werden als gegenständliche Modelle verstanden.
Gegenständliches Modell auf Basis eines theoretischen Modells
Auch für das Teilchenmodell kann ein gegenständliches Modell erzeugt werden, was analog zum theoretischen Modell aufgebaut ist. Eine Rüttelmaschine mit variabler Rüttelfrequenz (Modell für die Temperatur) , die Kugeln (Modell für Teilchen) in einem abgeschlossenen Raum umherwirbelt ist ein Beispiel für ein solches Modell. Mit diesem Modell können die Gasgesetze veranschaulicht werden.
Füllt man den Raum mit Kugeln zweier Größen kann auch verstanden werden, woher bei der brownschen Bewegung das ungeordnete Hin- und Herzappeln der mikroskopisch sichtbaren Teilchen kommt.
Die großen Kugeln (als Modell für mikroskopisch sichtbare Teilchen) werden ständig von den kleinen Kügelchen (als Modelle für submikroskopische Moleküle) gestoßen und so in Bewegung versetzt.
Modelle beruhen auf Annahmen
Modelle beruhen in der Regel auf bestimmten Annahmen und vernachlässigen bestimmte Aspekte. Das Teilchenmodell beruht u.a. auf den Annahmen, dass
- alle Stoffe aus kleinsten Teilchen bestehen,
- zwischen den Teilchen leerer Raum ist,
- die Teilchen sich gegenseitig anziehen,
- die Anziehungskraft mit zunehmendem Teilchenabstand kleiner wird,
- die Anziehungskraft stark vom Stoff und dessen Aggregatszustand abhängt.
Erklärungen und Vorhersagen durch Modelle
Mithilfe von Modellen lassen sich bestimmte Beobachtungen am Objekt erklären. So kannst du z.B. mit dem Teilchenmodell gut erklären, warum zum Zertrennen eines Festkörpers mehr Kraft aufzuwenden ist als zum Zertrennen einer Flüssigkeit.
Mit dem Teilchenmodell (dem theoretischen und seiner gegenständlichen Umsetzung) lassen sich der Gasdruck und qualitativ auch die Gasgesetze verstehen:
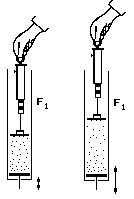
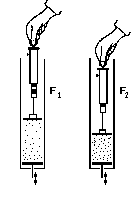
Zustandekommen des Gasdruckes:Ein Stempel schließt den "Gasraum" ab, sein Gewicht wird mit der Federwaage festgestellt. Erwärmt man das Modellgas (Erhöhung der Frequenz der schwingenden Bodenplatte), so steigt der "Druck" im Modellgas. Dieser Druck hat eine Kraft auf den Stempel zur Folge, was sich in einem geringeren Ausschlag der Federwaage zeigt. |
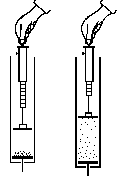 |
Gesetz von Boyle-MariotteBei konstanter "Temperatur" des Modellgases (d.h. Frequenz und Amplitude der schwingenden Platte sind fest). Ist der Druck des Modellgases umso größer, je kleiner das vom Gas eingenommene Volumen ist. Man erkennt als Folge des höheren Drucks im Modellgas den geringeren Ausschlag an der Federwaage. |
 |
Erläutere, wie man bei dem obigen Modellversuch vorgehen müsste, wenn man das Gesetz von GAY-LUSSAC veranschaulichen will.
Die obigen Überlegungen zeigen, dass die Wärmeerscheinungen, die wir in Versuchen beobachtet haben, gut mit dem Teilchenmodell verstanden werden können. Eine mechanistische Deutung der Wärmeerscheinungen ist hier möglich. Die Wärmelehre wird so zu einem Teilgebiet der Mechanik.
Dabeo kann die Temperatur eines Körpers als Maß für die mittlere Bewegungsenergie seiner Teilchen gedeutet werden.
Eigenschaften von Modellen
Modelle sollen verschiedene Eigenschaften besitzen, damit sie hilfreich beim Lernen und Erklären sind.
Einfach und anschaulich

Eine wichtige Forderung an ein Modell ist, dass es möglichst einfach und anschaulich ist. In unserem Teilchenmodell können wir uns z.B. sehr leicht überlegen, was mit dem Gas passiert, wenn sich der Stempel auf das Gas zu- bzw. von ihm wegbewegt (vergleiche auch die Bewegung eines Tennisschlägers in Bezug auf einen Tennisball):
Bewegt sich die Wand z.B. auf das Modellgas zu, so werden die Moleküle insgesamt schneller, die "Temperatur" des Modellgases steigt.
Produktiv und ausbaubar
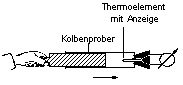
Wenn ein Modell produktiv und geeignet ist, dann muss die Vorhersage des Modells auch am Objekt, also bei einem realen Gas zutreffen. Schiebt man z.B. den Kolben auf das eingeschlossene Gas zu (d.h. nach rechts in der Abb.) so kann man mit dem Thermoelement tatsächlich eine Temperaturerhöhung im Gas feststellen.
Wir sehen also, dass unser Teilchenmodell in diesem Fall durchaus leistungsfähig war und wir durch das Modell Prognosen für das Verhalten in der Realität erstellen konnten. Das Teilchenmodell ist auch noch bei vielen anderen Phänomenen hilfreich und daher ausbaubar.
Ausbick
Modelle sind nicht nur in der Physik, sondern auch in den Naturwissenschaften allgemein, in der Wirtschaft und den Sozialwissenschaften von großer Bedeutung. So versuchen bspw. Forscher anhand von Klimamodellen die Erderwärmung besser zu verstehen, Auswirkungen der Erderwärmung vorherzusagen und mögliche Einflussparameter zur Reduktion der Erderwärmung zu finden. Auch Wettervorhersagen beruhen auf entsprechenden Modellen.