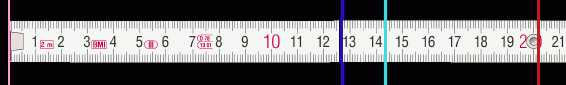In der Mitte des 19. Jahrhunderts hatte man die Atomspektren relativ genau untersucht. Großes Interesse galt dem sehr einfach aufgebauten atomaren Wasserstoff (\(\rm{H}\)). Hier machte sich insbesondere der schwedische Physiker Anders Jonas ÅNGSTRÖM (1814-1874) einen Namen. Er konnte bis 1866 die Wellenlängen der ersten vier sichtbaren Wasserstofflinien auf Bruchteile eines Prozents genau bestimmen.
Der schweizer Mathematiker Johann Jakob BALMER (1825-1898) fand 1884 ein Bildungsgesetz für die Werte dieser vier Wellenlängen, ohne allerdings eine physikalische Begründung für diese Gesetzmäßigkeit geben zu können.
Dem schwedischen Physiker Johannes Robert RYDBERG (1854-1919) gelang es schließlich 1888, eine einfachere Form für das Bildungsgesetz für die Werte dieser vier Wellenlängen zu finden. Seine Formel ist noch heute in fast allen Formelsammlungen zu finden. Aber auch RYDBERG konnte keine physikalische Begründug für seine Formel geben.
In diesem Artikel zeigen wir, wie man die Wellenlängen der ersten drei Wasserstofflinien im Schulunterricht mit der sogenannten BALMER-Röhre bestimmen kann. Außerdem führen wir in moderner Form vor, dass eine Gesetzmäßigkeit zwischen den Wellenlängen, genauer den zugehörigen Photonenenergieen besteht.
Aufbau und Durchführung
Die BALMER-Röhre ist eine wechselstrombetriebene Gasentladungsröhre mit Wasserdampffüllung. Die abgeschmolzene Röhre wird durch einen an hygroskopischer Grundlage gebundenen Wasservorrat mit Wasserdampf versorgt. Die Wassermoleküle werden durch die elektrische Entladung in atomaren Wasserstoff und Hydroxyl-Radikale aufgespalten. Eine hochtemperaturbeständige Kapillare im Innern der Lampe zwingt die Entladung auf einen engen Raum, so dass dort eine hohe Konzentration an atomarem Wasserstoff entsteht, der für die intensiven Spektrallinien verantwortlich ist; störende Banden, verursacht durch molekularen Wasserstoff, treten nicht auf.
Die Zerlegung des Lichts der BALMER-Röhre in Spektralfarben könnte durch ein Prisma geschehen. In dem in Abb. 4 dargestellten Versuchsaufbau betrachtet man das Licht der Röhre durch ein Gitter mit der Gitterkonstanten \(g=\frac{1}{570}\,\rm{mm}\), dass sich in einem Abstand von \(e=50{,}0\,\rm{cm}\) von der Röhre befindet (subjektive Beobachtungsmethode).
Beim Blick durch das Gitter sieht man links und rechts von der rosa leuchtenden Röhre drei farbige Linien, welche virtuelle Bilder der Spektralröhre darstellen. Diese Linien stellen das Spektrum des atomaren Wasserstoffs dar.
Misst man nun die Abstände \(a_{\rm{rot}}\), \(a_{\rm{türkis}}\) und \(a_{\rm{blau}}\) der virtuellen Bilder von der Spektralröhre, so lassen sich mit der bekannten Formel für die Wellenlängenbestimmung mit einem Gitter\[\lambda = \frac{g \cdot {a}}{\sqrt{e^2+{a}^2}}\]die Wellenlängen der Spektrallinien berechnen.
Beobachtung
Wie oben bereits gesagt sieht man beim Blick durch das Gitter links und rechts von der rosa leuchtenden Röhre jeweils drei farbige Linien, welche virtuelle Bilder der Spektralröhre darstellen. Diese Linien zeigen drei der vier sichtbaren Linien des Spektrums von atomarem Wasserstoff.
Abb. 7 zeigt links beim Nullpunkt des Lineals die rosa leuchtende Röhre und rechts die virtuellen Bilder der drei sichtbaren Spektrallinien.
Auswertung (Teil 1)
Aufgabe
Entnimm der Abb. 7 die Abstände \(a_{\rm{rot}}\), \(a_{\rm{türkis}}\) und \(a_{\rm{blau}}\).
Berechne die zugehörigen Wellenlängen.
ÅNGSTRÖM hatte bis 1866 nicht nur drei, sondern vier Linien beobachten können (Abb. 8) und die zugehörigen Wellenlängen, die er mit \(\mathrm{H}_\alpha\), \(\mathrm{H}_\beta\), \(\mathrm{H}_\gamma\) und \(\mathrm{H}_\delta\) bezeichnete, mit noch größerer Genauigkeit bestimmt (Tab. 1).
| Name | \(\mathrm{H}_\alpha\) | \(\mathrm{H}_\beta\) | \(\mathrm{H}_\gamma\) | \(\mathrm{H}_\delta\) |
|---|---|---|---|---|
| Farbe | rot | türkis | blau | violett |
| \(\lambda\) in \(\rm 10^{-10}\,m\) | \(6562{,}1\) | \(4860{,}7\) | \(4340{,}1\) | \(4101{,}2\) |
Auswertung (Teil 2)
Aufgabe
Berechne z.B. mit Hilfe einer Tabellenkalkulation zu den Wellenlängen in Tab. 1a die zugehörigen Photonenenergien.
| Name | \(\mathrm{H}_\alpha\) | \(\mathrm{H}_\beta\) | \(\mathrm{H}_\gamma\) | \(\mathrm{H}_\delta\) |
|---|---|---|---|---|
| Farbe | rot | türkis | blau | violett |
| \(\lambda\) in \(\rm 10^{-10}\,m\) | \(6562{,}1\) | \(4860{,}7\) | \(4340{,}1\) | \(4101{,}2\) |
| \(E_{\rm{Ph}}\) in \(\rm{eV}\) |
Bestätige rechnerisch, dass sich die Photonenenergien aus Tab. 1c relativ genau durch das Bildungsgesetz\[{E_{{\rm{Ph}}}} = 13{,}6057\,{\rm{eV}} \cdot \left( {\frac{1}{{{2^2}}} - \frac{1}{{{n^2}}}} \right)\;;\;n \in \left\{ {3\;;\;4\;;\;5\;;\;6} \right\}\]ergeben, wobei für den Wert \(13{,}6057\,{\rm{eV}}\) gilt\[\frac{e^4 \cdot m_{\rm{e}}}{8 \cdot {\varepsilon_0}^2 \cdot h^2}=13{,}6057\,{\rm{eV}}\]
BALMER glaubte fest an eine Gesetzmäßigkeit, mit der sich die Wellenlängen berechnen lassen sollten. Er schreibt: "Es müßte eine einfache Formel geben, mit Hülfe derer die Wellenlängen der vier ausgezeichneten Wasserstofflinien sich darstellen ließen." BALMER fand dieses Bildungsgesetz durch Zahlenspielerei und Probieren. Er erkannte zuerst, dass sich die Verhältnisse je zweier Wellenlängen relativ einfach durch die Verhältnisse kleiner Zahlen ausdrücken lassen:\[\frac{\lambda \left( \rm{H}_\alpha \right)}{\lambda \left( \rm{H}_\delta \right)} = \frac{8}{5} \quad;\quad \frac{\lambda \left( \rm{H}_\alpha \right)}{\lambda \left( \rm{H}_\beta \right)} = \frac{27}{20} \quad;\quad \frac{\lambda \left( \rm{H}_\beta \right)}{\lambda \left( \rm{H}_\delta \right)} = \frac{32}{27}\quad;\quad ...\]Dann gelang es BALMER "einen gemeinschaftlichen Faktor aufzusuchen, der zu den Wellenlängen in möglichst einfachen Zahlenverhältnissen stund." Für diesen gemeinsamen Faktor \(A\) ergibt sich\[A = 3645{,}06 \cdot 10^{-10}\,\rm{m}\]Mit diesem Faktor \(A\) berechnete BALMER nun\[\lambda \left( \rm{H}_\alpha \right) = \frac{9}{5} \cdot A \quad;\quad \lambda \left( \rm{H}_\beta \right) = \frac{4}{3} \cdot A \quad;\quad \lambda \left( \rm{H}_\gamma \right) = \frac{25}{21} \cdot A \quad;\quad \lambda \left( \rm{H}_\delta \right) = \frac{9}{8} \cdot A\]Erweitert man den zweiten und den vierten Faktor jeweils mit \(4\), so liefern alle vier Faktoren die Zahlenreihe \({\frac{9}{5}}\), \({\frac{16}{12}}\), \({\frac{{25}}{{21}}}\) und \({\frac{{36}}{{32}}}\). Diese Zahlenreihe lässt sich aber einfach berechnen durch\[\frac{n^2}{n^2 - 4}\;;\; n \in \left\{ {3\;;\;4\;;\;4\;;\;6} \right\}\]Damit erhielt BALMER das von ihm gesuchte Bildungsgesetz\[\lambda = A \cdot \left( {\frac{{{n^2}}}{{{n^2} - 4}}} \right)\;;\;n \in \left\{ {3\;;\;4\;;\;4\;;\;6} \right\} \quad (1)\]RYDBERG konnte dieses Bildungsgesetz vereinfachen, indem er statt der Wellenlänge \(\lambda\) deren Kehrwert \(\frac{1}{\lambda}\) betrachtete. Für diesen Kehrwert gilt nach Gleichung \((1)\)\[\begin{eqnarray}\frac{1}{\lambda } &=& \frac{1}{A} \cdot \frac{{{n^2} - 4}}{{{n^2}}}\\ &=& \frac{1}{A} \cdot \left( {1 - \frac{4}{{{n^2}}}} \right)\\ &=& \frac{1}{A} \cdot \left( {\frac{4}{4} - \frac{4}{{{n^2}}}} \right)\\ &=& \frac{4}{A} \cdot \left( {\frac{1}{4} - \frac{1}{{{n^2}}}} \right)\\ &=& \frac{4}{A} \cdot \left( {\frac{1}{{{2^2}}} - \frac{1}{{{n^2}}}} \right)\;;\;n \in \left\{ {3\;;\;4\;;\;4\;;\;6} \right\}\end{eqnarray}\]Den Wert \[\frac{4}{A}=\frac{4}{3645{,}06 \cdot 10^{-10}\,\rm{m}}=1{,}0974 \cdot 10^{7}\,\frac{1}{\rm{m}}\]bezeichnet man heutzutage als RYDBERG-Konstante \(R_{\infty}=1{,}0974 \cdot 10^{7}\,\frac{1}{\rm{m}}\).
Ergebnis
Die Wellenlängen der vier sichtbaren Linien des Spektrums von atomarem Wasserstoff (\(\rm{H}\)) lassen sich durch ein Bildungsgesetz berechnen. Dies lässt darauf schließen, dass die Wellenlängen nicht zufällig sind, sondern durch physikalische Gesetzmäßigkeiten bestimmt werden.