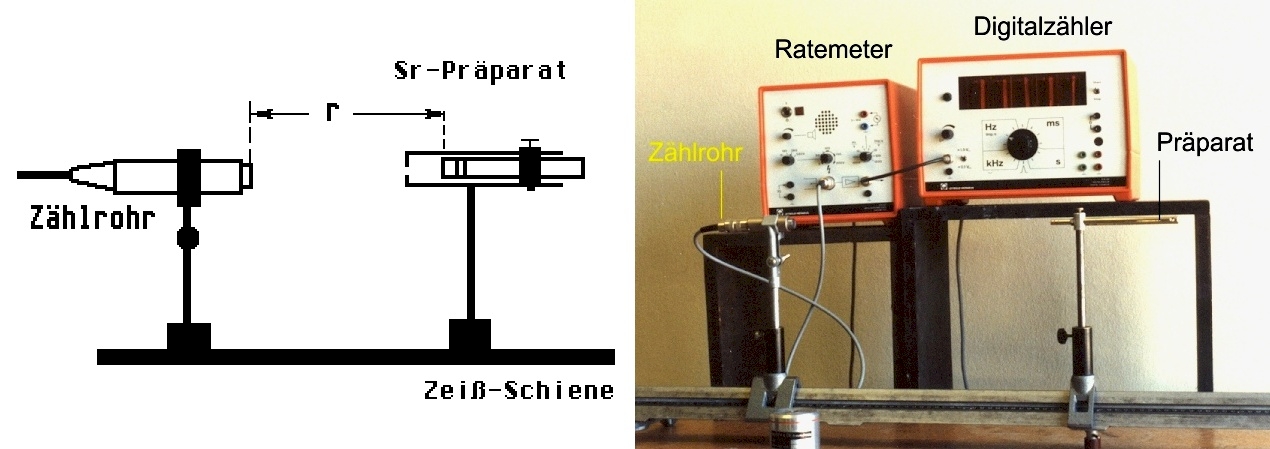
Aufbau und Durchführung
Man untersucht die Zählrate \(R\) (Torzeit z.B. \(100\,\rm{s}\)) in Abhängigkeit vom Abstand \(r\).
Beobachtung
| Abstand \(r\) in \(\rm{cm}\) | \(5\) | \(10\) | \(20\) | \(25\) | \(30\) | \(40\) | \(70\) |
|---|---|---|---|---|---|---|---|
| Zählrate \(R\) in \(\frac{1}{\rm{s}}\) | \(329\) | \(93{,}0\) | \(39{,}5\) | \(20{,}6\) | \(14{,}7\) | \(5{,}2\) | \(1{,}8\) |
Auswertung
Aufgabe
Trage die Ergebnisse in einfach logarithmischem Papier auf oder bearbeite das Ergebnis mit einem Tabellenkalkulationsprogramm (z.B. Excel) entsprechend.
Bestimme die Steigung und zeige \(R \sim \frac{1}{{{r^2}}}\).
Erläutere, warum man daraus schließen kann , das die harte β-Strahlung des Strontiums im untersuchten Bereich von Luft nur unwesentlich absorbiert wird.
Ergebnis
Die Zählrate \(R\) von (harter) \(\beta\)-Strahlung, die kaum von Luft absorbiert wird, sinkt umgekehrt proportional zum Abstand \(r\) von der Strahlungsquelle:\[R \sim \frac{1}{r^2}\]