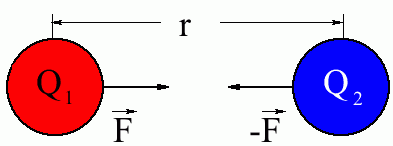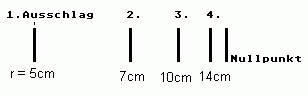Eine punktförmige Ladung erzeugt ein radialsymmetrisches Feld. Bringt man in dieses Feld eine weitere Punktladung, so kommt es zu einer Kraftwirkung, welche sich relativ einfach durch das Gesetz von COULOMB beschreiben lässt. Die experimentelle Untersuchung ist mit verschiedenen Versuchsanordnungen möglich. Es wird von der Ausstattung der Schule abhängen, wie genau die Kraftwirkung zwischen den Punktladungen bestimmt werden kann.
Qualitative Untersuchung der Kraftwirkung mit der Drehwaage
Aufbau und Durchführung
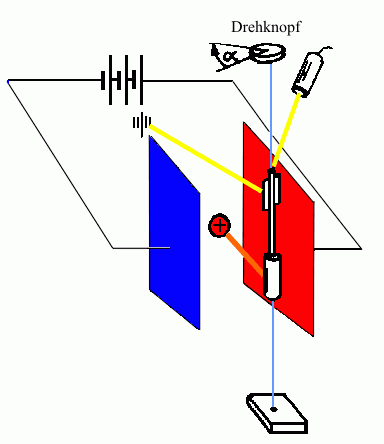
Eine metallene Kugel ist mit einem Isolierstil am Torsionsfaden befestigt, dessen Drehwinkel mit einem daran befestigten Spiegel und einem Lichtzeiger kontrolliert wird. Dabei ist die rücktreibende Kraft auf Grund des hookeschen Gesetzes zum Drehwinkel direkt proportional. Die Kugel wird mittels Hochspannungsquelle (Influenzmaschine, Bandgenerator etc) geladen. Eine zweite geladene Kugel wird ihr genähert, wobei die Kraft auf die Kugel in Abhängigkeit vom Mittelpunktsabstand (und eventuell auch in Abhängigkeit von der Kugelladung) untersucht wird.
Es gibt nun zwei Möglichkeiten der Kraftmessung:
- Man dreht jeweils der Torsionskopf oben soweit nach, bis der Lichtzeiger wieder an der Ausgangsstelle steht. Dabei kann man die Mittelpunktsabstände \(r\) der Kugeln klar bestimmen. Die Kraft ist dann direkt proportional zur Weite \(\alpha \) des Drehwinkel des Torsionskopfs. Diese Winkelweite ist meist sehr gering und deshalb wenig zufriedenstellend genau zu bestimmen.
- Man lässt die Kugel "auswandern" und misst die Abstände des Lichtzeigers von der Ausgangsstellung. Dabei ergeben sich wegen des Auswanderns der drehbaren Kugel Ungenauigkeiten in der Abstandsbestimmung. Andererseits ist dieser Versuch wesentlich zügiger durchzuführen als der mittels Verdrehen des Torsionskopfs und leidet deshalb nicht so unter dem Ladungsabfluss während der Versuchsreihe. Da die Lichtzeigerausschläge bei den vorkommenden kleinen Winkelweiten (< 5°) direkt proportional zur Winkelweite und damit zur Kraft sind, bringt diese Messmethode im Schulversuch die besseren Ergebnisse.
Aufgabe
Auswertung
Beim Versuch mit der Drehwaage nach der 2. Methode wurde der Abstand \(r\) zwischen den Kugeln bei gleichbleibender Ladung beider Kugeln variiert und der zugehörige Ausschlag des Lichtzeigers mittels Bleistiftstrich auf einem Papier an der Wand festgehalten (siehe Abb. 4).
Untersuche, welche Proportionalität sich aus den Beobachtungen ergibt.
Quantitative Untersuchung der Kraftwirkung mit dem elektronischen Kraftmesser
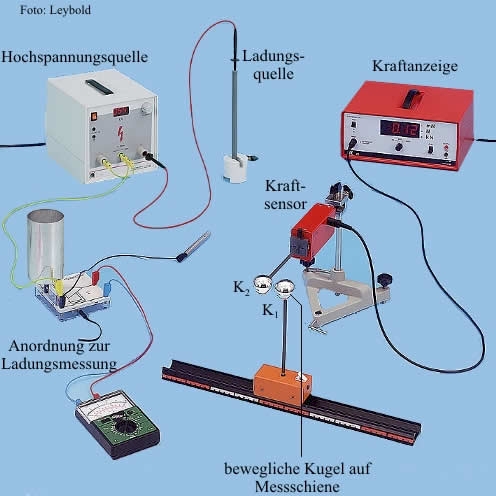
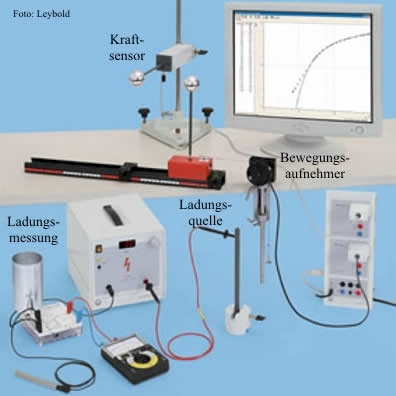
Statt der Drehwaage, kann natürlich auch ein Kraftsensor verwendet werden, der praktisch nicht ausweicht. An diesem befestigt man eine metallene Kugel an einem Isolierstil und nähert eine zweite Kugel längs einer Messschiene (siehe nebenstehendes Bild).
- Die Kugeln werden mit einem Stift (Ladungsquelle) berührt. Dieser Stift ist mit einem Pol der Hochspannungsquelle verbunden.
- Die Kugel wird in das Innere eines Faradaybechers gebracht. Mit einem Operationsverstärker samt Messgerät gelingt dann die Messung der auf der Kugel sitzenden Ladung.
- Über den Kraftsensor samt Anzeigegerät gelingt es, die Kraft, welche an der ortsfesten (linken) Kugel angreift festzustellen. Durch Variation des Abstandes \(r\) zwischen den beiden Kugelmitten können die folgenden Messwerte aufgenommen werden.
Teilversuch 1: Die Ladungen Q1 und Q2 auf den Kugeln K1 und K2 sind fest, der Abstand \(r\) der Kugeln wird variiert.
| \(r\;{\rm{in}}\;{\rm{cm}}\) | \(4,0\) | \(5,0\) | \(6,0\) | \(7,0\) | \(8,0\) | \(9,0\) | \(10\) | \(15\) | \(20\) | \(25\) |
| \(F\;{\rm{in}}\;{\rm{mN}}\) (\({Q_1} > 0\) und \({Q_2} > 0\)) | \(3,41\) | \(2,73\) | \(2,40\) | \(1,94\) | \(1,33\) | \(0,95\) | \(0,84\) | \(0,41\) | \(0,21\) | \(0,11\) |
| \(F\;{\rm{in}}\;{\rm{mN}}\) (\({Q_1} < 0\) und \({Q_2} > 0\)) | \(-3,6\) | \(-2,95\) | \(2,49\) | \(-2,11\) | \(-1,56\) | \(-1,36\) | \(-0,96\) | \(-0,42\) | \(-0,17\) | \(-0,12\) |
Aufgabe
Werte die obigen Messwerte aus.
Teilversuch 2: Die Ladungen Q1 und Q2 auf den Kugeln K1 und K2 werden variiert, der Abstand \(r\) der Kugeln bleibt fest.
a) COULOMB-Kraft \(F\) auf die Kugel 2 in Abhängigkeit von ihrer Ladung \(Q_2\) bei \(Q_2 > 0\), \(Q_1 = 36\rm{nAs}\) und \(d = 6\rm{cm}\)
| \(Q_2\;{\rm{in}}\;{\rm{nAs}}\) | \(7\) | \(14\) | \(22\) | \(28\) | \(36\) |
| \(F\;{\rm{in}}\;{\rm{mN}}\) | \(0,32\) | \(0,91\) | \(1,40\) | \(2,01\) | \(2,76\) |
b) COULOMB-Kraft \(F\) auf die Kugel 2 in Abhängigkeit von der Ladung \(Q_1\) der Kugel 1 bei \(Q_1<0\), \(Q_2 = 36\rm{nAs}\) und \(d = 6\rm{cm}\)
| \(Q_1\;{\rm{in}}\;{\rm{nAs}}\) | \(-7\) | \(-14\) | \(-22\) | \(-28\) | \(-36\) |
| \(F\;{\rm{in}}\;{\rm{mN}}\) | \(-0,40\) | \(-0,96\) | \(-1,39\) | \(-2,10\) | \(-2,65\) |
Aufgabe
Werte die obigen Messwerte aus.
Auswertung des Versuchs mittels Computer (Messwerterfassungssystem)
Bei der Auswertung des Versuchs mittels Computer (Messwerterfassungssystem) wird die Kraft über eine vom Kraftsensor abgegebene Spannung auf die vertikale Achse, der Mittelpunktsabstand der Kugeln mittels Bewegungsmesswandler als Spannung auf die horizontale Achse gelenkt. Die Messpunkte und die erwartete \(\frac{1}{{{r^2}}}\)-Kurve stimmen für kleine Abstände nicht mehr gut überein, da in diesem Bereich zusätzlich zu den rein abstoßenden Kräften auch anziehende Kräfte auf Grund von Influenz auftreten.
Der Vorteil des Computereinsatzes besteht darin, dass die Messwerte sofort gespeichert werden und die graphische Auswertung sehr leicht durchzuführen ist.