\[\frac{{{E_1}^\prime }}{{{E_1}}} = \frac{{\frac{1}{2} \cdot {m_1} \cdot {{v^\prime}^2}}}{{\frac{1}{2} \cdot {m_1} \cdot {v_1}^2}} = \frac{{{{v^\prime}^2}}}{{{v_1}^2}} = \frac{{{{\left( {\frac{{{m_1} \cdot {v_1} + {m_2} \cdot {v_2}}}{{{m_1} + {m_2}}}} \right)}^2}}}{{{v_1}^2}}\]Wegen \({v_2} = 0\) ergibt sich\[\frac{{{E_1}^\prime }}{{{E_1}}} = \frac{{{{\left( {\frac{{{m_1} \cdot {v_1} + {m_2} \cdot 0}}{{{m_1} + {m_2}}}} \right)}^2}}}{{{v_1}^2}} = \frac{{{{\left( {\frac{{{m_1} \cdot {v_1}}}{{{m_1} + {m_2}}}} \right)}^2}}}{{{v_1}^2}} = \frac{{{{\left( {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \right)}^2} \cdot {v_1}^2}}{{{v_1}^2}} = {\left( {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \right)^2} = \frac{{{m_1}^2}}{{{{\left( {{m_1} + {m_2}} \right)}^2}}}\]Dividiert man Zähler und Nenner des Bruches durch \({m_1}^2\) ergibt sich\[\frac{{{E_1}^\prime }}{{{E_1}}} = \frac{{{m_1}^2:{m_1}^2}}{{{{\left( {{m_1} + {m_2}} \right)}^2}:{m_1}^2}} = \frac{1}{{{{\left( {1 + \frac{{{m_2}}}{{{m_1}}}} \right)}^2}}} = \frac{1}{{{{\left( {1 + \frac{1}{{\frac{{{m_1}}}{{{m_2}}}}}} \right)}^2}}}\]
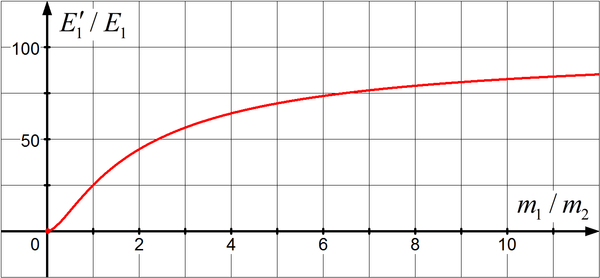
Aus dem Kurvenverlauf kann man erkennen, dass der Körper 1 umso mehr Energie behält je größer das Massenverhältnis \(\frac{{{m_1}}}{{{m_2}}}\) ist. Die Werte der \({E_1}'/{E_1}\)-Achse sind in \(\% \) angegeben.