Innere Energie - Wärmekapazität

Erhitzen eines Gegenstandes mit bekannter Masse und Wärmekapazität

Joachim Herz Stiftung

Man bringt in die Flamme des Gaskochers eine Metallkugel und wartet so lange, bis die Kugel die Flammentemperatur angenommen hat.

Wenn du jetzt eine Idee hast, so bringe sie zu Papier und vergleiche dann mit unserem Lösungsvorschlag (Vorgehensweise, Messgrößen, Bestimmung der Flammentemperatur aus den Messgrößen).

Ermitteln der Mischtemperatur mit Wasser

Man führt einen "Mischversuch" mit der auf etwa Flammentemperatur befindlichen Kugel und dem Wasser in einem Kalorimetergefäß durch.

Bringe nun deine Lösung zu Papier und vergleiche dann mit unserem Lösungsvorschlag (Bestimmung der Flammentemperatur aus den Messgrößen).

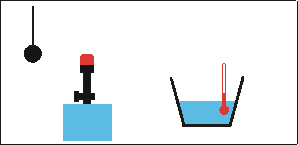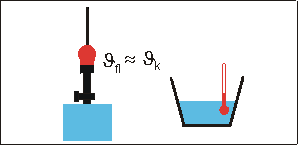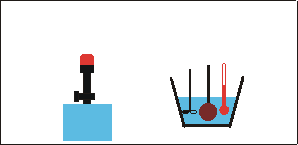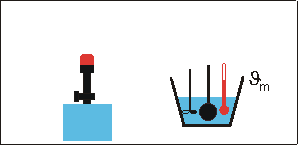
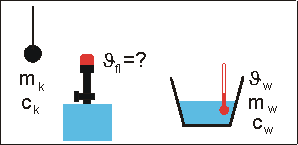Versuchsaufbau und -durchführung

Zur Abschätzung der Flammentemperatur bringt man eine Metallkugel (Masse m_k, spezifische Wärmekapazität c_k) in die Flamme. Nach kurzer Zeit hat die Kugel die Temperatur der Flamme angenommen (Metalle sind gute Wärmeleiter).

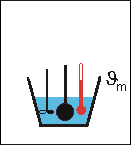
Dann bringt man die glühende Kugel schnell in ein Wasserbad (Wassermasse m_w, Wassertemperatur ϑ_w, spezifische Wärmekapazität c_w) und stellt nach dem Umrühren die Mischtemperatur ϑ_m fest.

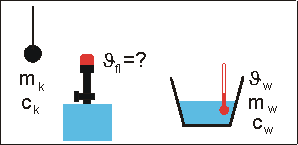
Versuchsauswertung

Nach dem Energieerhaltungssatz gilt
\[\Delta {E_{{\rm{i}}{\rm{,ab}}}} = \Delta {E_{{\rm{i}}{\rm{,auf}}}} \Leftrightarrow {m_{\rm{K}}} \cdot {c_{\rm{K}}} \cdot \left( {{\vartheta _{\rm{K}}} - {\vartheta _{\rm{M}}}} \right) = {m_{\rm{W}}} \cdot {c_{\rm{W}}} \cdot \left( {{\vartheta _{\rm{M}}} - {\vartheta _{\rm{W}}}} \right) \Leftrightarrow {\vartheta _{\rm{K}}} - {\vartheta _{\rm{M}}} = \frac{{{m_{\rm{W}}} \cdot {c_{\rm{W}}} \cdot \left( {{\vartheta _{\rm{M}}} - {\vartheta _{\rm{W}}}} \right)}}{{{m_{\rm{K}}} \cdot {c_{\rm{K}}}}} \Leftrightarrow {\vartheta _{\rm{K}}} = \frac{{{m_{\rm{W}}} \cdot {c_{\rm{W}}} \cdot \left( {{\vartheta _{\rm{M}}} - {\vartheta _{\rm{W}}}} \right)}}{{{m_{\rm{K}}} \cdot {c_{\rm{K}}}}} + {\vartheta _{\rm{M}}}\]

Beispiel: \({m_{\rm{K}}} = 30,6{\rm{g}}\), \({c_{\rm{K}}} = 0,46\frac{{\rm{J}}}{{{\rm{g}} \cdot {\rm{^\circ C}}}}\), \(300{\rm{g}}\), \({{\vartheta _{\rm{W}}} = 17,2^\circ {\rm{C}}}\), \({c_{\rm{W}}} = 4,19\frac{{\rm{J}}}{{{\rm{g}} \cdot {\rm{^\circ C}}}}\) und \({{\vartheta _{\rm{M}}} = 30,0^\circ {\rm{C}}}\). Dann ergibt sich für \({{\vartheta _{\rm{K}}}}\)
\[{\vartheta _{\rm{K}}} = \frac{{300{\rm{g}} \cdot 4,19\frac{{\rm{J}}}{{{\rm{g}} \cdot {\rm{^\circ C}}}} \cdot \left( {30,0^\circ {\rm{C}} - 17,2^\circ {\rm{C}}} \right)}}{{30,6{\rm{g}} \cdot 0,46\frac{{\rm{J}}}{{{\rm{g}} \cdot {\rm{^\circ C}}}}}} + 30,0^\circ {\rm{C}} = 1,2 \cdot {10^3}^\circ {\rm{C}}\]
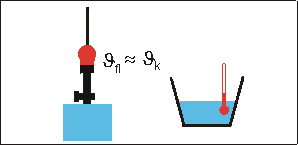
Da die Flammentemperatur ungefähr gleich der Temperatur der Kugel vor dem Mischen ist, kann man sagen, dass die Flamme etwas über \({1000^\circ {\rm{C}}}\) heiß ist.