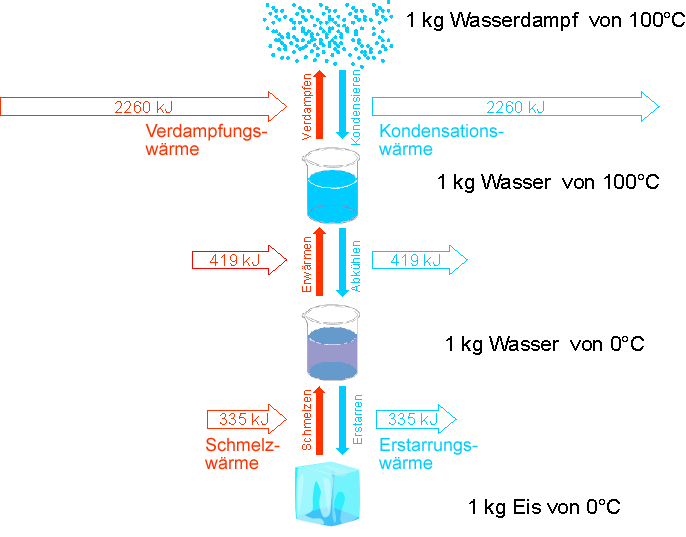
Spezifische Schmelz- und Verdampfungswärme von Eis bzw. Wasser
Hinweis: Schmelzwärme und Verdampfungswärme werden teilweise auch als Schmelzenergie und Verdampfungsenergie bezeichnet. Für \(1\,\rm{kg}\) Wasser sind in dem folgenden Diagramm die wichtigen Energien angegeben.
Im Diagramm ist zu sehen, dass Verdampfungsenergie und Kondensationsenergie bzw. Schmelzenergie und Erstarrungsenergie gleich groß sind.
Notwendige und freiwerdende Energie bei Phasenübergängen sind gleich
Kühlst du also ein Gas ab, so kondensiert dieses bei der Kondensationstemperatur. Beim Kondensieren wird Energie frei. Um den Stoff wieder zu verdampfen, ist die gleiche Energie nötig. Die Kondensationsenergie ist gleich der Verdampfungsenergie.
Kühlst du eine Flüssigkeit ab, so erstarrt diese bei der Erstarrungstemperatur. Beim Erstarren wird ebenfalls Energie frei. Um den Stoff wieder zu schmelzen, ist die gleiche Energie nötig. Die Erstarrungsenergie ist gleich der Schmelzenergie.
Allgemein gilt
- Bei Übergängen, an denen die Bindung der Teilchen zueinander loser wird, muss Energie hinzugefügt werden (fest->flüssig, flüssig->gasförmig, fest->gasförmig).
- Bei Übergängen, an denen die Bindung der Teilchen zueinander fester wird, wird Energie frei (gasförmig->flüssig, flüssig->fest, gasförmig->fest).
Hinweis: Die Schmelz- und Verdampfungswärme von Wasser sind relativ groß. Die Energie, die du aufwenden musst, um \(1\,\rm{kg}\) Eis zu schmelzen, entspricht der Energie, die nötig ist, um \(1\,\rm{kg}\) Wasser von \(0^\circ {\rm{C}}\) auf etwa \(80^\circ {\rm{C}}\) zu erwärmen.
Spezifische Schmelz- und Verdampfungswärme
Willst du berechnen, wie viel Energie notwendig ist, um einen reinen Festkörper, eine reine Flüssigkeit bzw. ein reines Gas zu erwärmen (ohne Phasenübergang!), so benutzt man die Beziehung: \[\Delta E_{\rm{i}} = c \cdot m \cdot \Delta \vartheta .\] Dabei ist für \(c\) jeweils die spezifische Wärmekapazität von Festkörper, Flüssigkeit oder Gas einzusetzen.
Um zu berechnen, wie viel Energie zum Schmelzen bzw. Verdampfen aufzuwenden ist, kannst du die folgenden Beziehungen nutzen: \[\Delta E_{\rm i}= s\cdot m\qquad\rm{bzw.}\qquad \Delta E_{\rm i}= r\cdot m\] Dabei stellen \(s\) bzw. \(r\) jeweils die spezifische Schmelz- bzw. Verdampfungswärme dar. Ihre Einheit ist \(\rm{\frac{J}{g}}\) (oder auch \(\rm{\frac{kJ}{g}}\)).
Einen Versuch zur Bestimmung der Schmelzwärme findest du hier. Einen Versuch zur Bestimmung der Verdampfungswärme hier.
Eine Liste mit Tabellenwerten für spezifische Schmelz- und Verdampfunsenergien findest du bei Wikipedia: Liste der Schmelzenergien ; Liste der Verdampfungsenergieen