Volumenänderung von Flüssigkeiten
Wenn man Flüssigkeiten erwärmt, dann dehnen sie sich im Allgemeinen in alle Richtungen aus, wenn man sie abkühlt, dann ziehen sie sich im Allgemeinen in alle Richtungen zusammen.
Verschiedene Flüssigkeiten dehnen sich beim Erwärmen unterschiedlich stark aus und ziehen sich beim Abkühlen auch unterschiedlich stark zusammen. Dieses unterschiedliche Verhalten verschiedener Flüssigkeiten beschreiben wir durch den sogenannten Volumenausdehnungskoeffizient \(\gamma\); er gibt an, um welchen Bruchteil des Volumens bei \(0^\circ {\rm{C}}\) sich eine Flüssigkeit bei der Erwärmung auf \(1^\circ {\rm{C}}\) ausdehnt; für die Maßeinheit des Volumenausdehnungskoeffizienten gilt \(\left[ \gamma \right] = \frac{1}{{^\circ {\rm{C}}}}\).
Eine Ausnahme bildet Wasser; es zieht sich beim Erwärmen zwischen \(0^\circ {\rm{C}}\) und \(4^\circ {\rm{C}}\) zusammen. Man bezeichnet diese Verhalten von Wasser als Anomalie des Wassers (anomal: gegen die Regel).
Nachweis der Volumenausdehnung von Flüssigkeiten
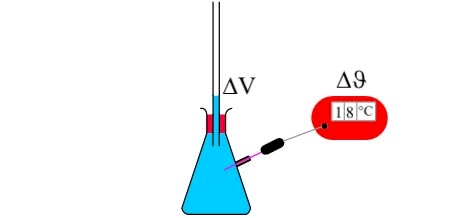
Die Volumenausdehnung von Flüssigkeiten kannst du wie in der Animation dargestellt relativ einfach untersuchen. Dazu setzt du auf einen mit Flüssigkeit gefüllten Glaskolben ein enges Steigrohr (Kapillarrohr). Nun erwärmst du die Flüssigkeit im Kolben bspw. mit Hilfe eines Bunsenbrenners. Die sich ergebende Volumenänderung kannst du nun am Steigrohr beobachten.
Raumausdehnungskoeffizient
Für verschiedene Flüssigkeiten im Kolben kannst du verschiedene Volumenänderungen feststellen. Die Grafik in Abb. 2 vergleicht die Volumenänderungen verschiedener Flüssigkeiten.
Mit Hilfe des Experimentes kannst Du, bei bekannter Geometrie des Steigrohres, auch den sog. Raumausdehnungskoeffizienten \(\gamma\) bestimmten. Dieser Wert ist eine Materialkonstante und gibt an, wie stark sich ein Stoff bei der Erwärmung um ein Kelvin relativ zu seinem Ausgangsvolumen ausdehnt. Du kannst ihn berechnen mit der Formel \[\gamma=\frac{\Delta V}{ {V_0} \cdot \Delta \vartheta}\]
wobei \(V_0\) das Ausgangsvolumen, \(\Delta V\) die Volumenänderung und \(\Delta \vartheta\) die Temperaturänderung ist.
Bei bekanntem Ausdehnungskoeffizienten kannst du mithilfe von \(\Delta V = {\gamma _{{\rm{Flüssigkeit}}}} \cdot {V_0} \cdot \Delta \vartheta\) auch Volumenausdehnungen berechnen.
Anomalie des Wassers
Viele Flüssigkeiten dehnen sich regulär aus, d.h. die Volumenänderung \(\Delta V\) ist proportional zur Temperaturänderung \(\Delta \vartheta\). Die für uns wichtigste Flüssigkeit, das Wasser, zeigt allerdings im Temperaturbereich knapp über dem Gefrierpunkt ein anomales Ausdehnungsverhalten.
Beispiele für Anwendungen
Die Volumenausdehnung von Flüssigkeiten wird in einer Reihen von technischen Anwendungen genutzt. Beispiele sind Flüssigkeitsthermometer, Sprinkleranlagen und Thermostatventile.
Aufgabe
Du hast, wie im Bild dargestellt, einen mit einer Flüssigkeit gefüllten Glaskolben, auf dem sich ein enges Steigrohr mit bekanntem Innendurchmesser befindet. Nun wird die Flüssigkeit mit einem Bunsenbrenner um 10°C erwärmt. Markiere alle zutreffenden Aussagen.