Sehr genaue Untersuchungen über den Zerfall von schnellen Myonen wurden 1975 bei CERN in der Nähe von Genf angestellt:
Pionen (Elementarteilchen, die mit Hilfe von Protonen erzeugt wurden), zerfallen in sehr kurzer Zeit in Myonen.
Hier die Gleichungen für den Zerfall von negativen Pionen und negativen Myonen:
\[ \begin{array}{} \pi^- \quad \rightarrow \quad \mu^- + \overline{\nu}_{\mu} \\
\mu^- \quad \rightarrow e^- + \nu_{\mu} + \overline{\nu}_e \end{array} \]
Bei CERN wurden die Myonen, die mit \(v=0{,}99942 \cdot c\) nahezu Lichtgeschwindigkeit hatten, in einem Speicherring auf Kreisbahnen gehalten und der Zerfall der Myonen mit Hilfe von Elektronendetektoren (Myonen zerfallen in Elektronen und verschiedene Neutrinosorten) beobachtet.
Abb. 1 zeigt den prinzipiellen Aufbau des Speicherrings, der einen Durchmesser von ca. \(14\,\rm{m}\) hatte.
Die Myonen laufen in einer kreisförmigen Vakuumröhre. Damit sich die geladenen Myonen auf Kreisbahnen bewegen sind insgesamt 40 Ablenkmagnete (rot) um die Vakuumröhre angeordnet. Im Innenraum befinden sich Detektoren (blau), welche die Elektronen, die beim Myonenzerfall entstehen, nachweisen können.
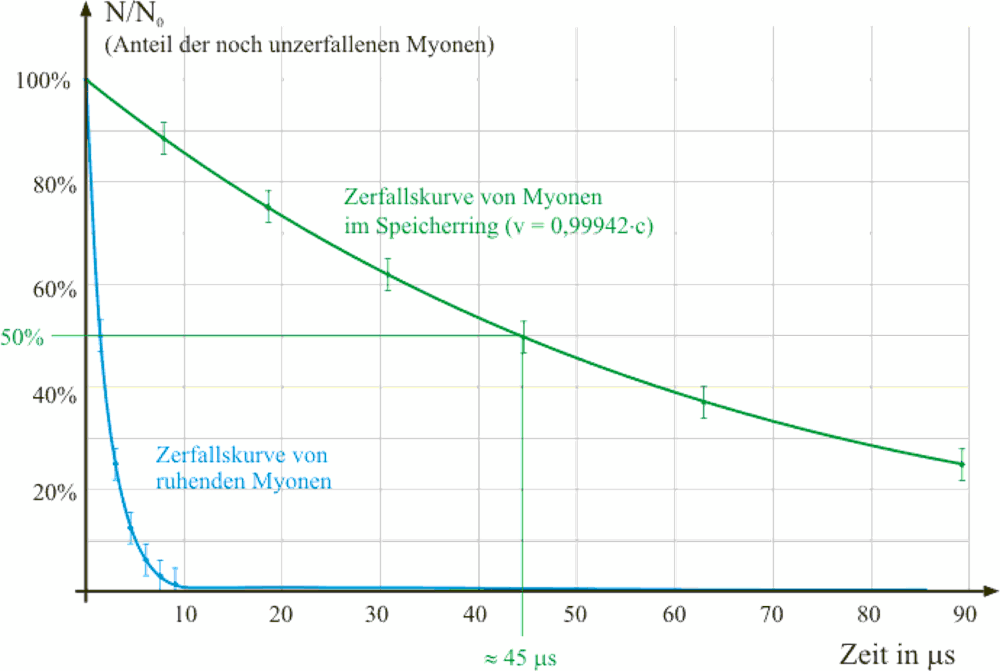
Die im Speicherring kreisenden Myonen zerfielen aufgrund der Zeitdilatation (die Myonen können als bewegte Uhren aufgefasst werden) mit einer Halbwertszeit von \(44{,}6\,\rm{\mu s}\) (vgl. grüne Kurve in dem Diagramm links). Dies ist eine deutlich längere Zeit als die Halbwertszeit von \(1{,}52\,\rm{\mu s}\) die man für langsame Myonen feststellt. Bei der Messung der Halbwertszeit der schnellen Myonen konnte man den Messfehler unter \(1\%\) halten.
Der Versuch stellt eine sehr genaue experimentelle Bestätigung der von EINSTEIN theoretisch vorhergesagten Zeitdilatation dar:
\[ T_{1/2} = T_{1/2}' \cdot \sqrt{1 - \left( \frac{v}{c} \right)^2 } \\
T_{1/2} = 44{,}6\,\rm{\mu s} \cdot \sqrt{1 - 0{,}99942^2} = 1{,}52\,\rm{\mu s}\]