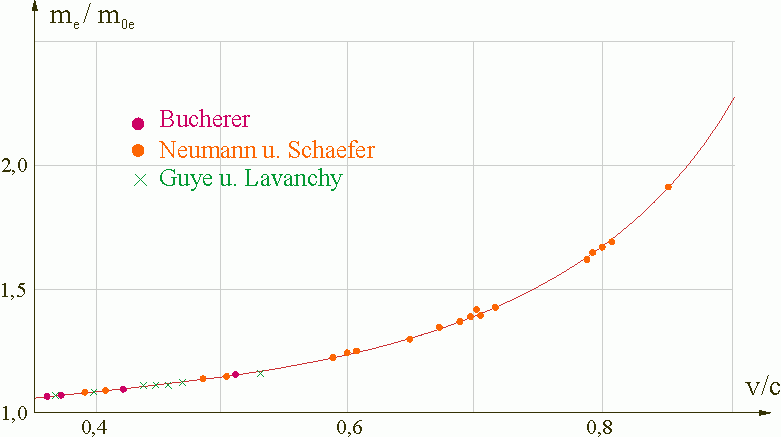
Im Versuch von BUCHERER (Link am Ende dieses Artikels) wird über die exakte Bestimmung der spezifischen Elektronenladung \(\frac{e}{m}\) bei unterschiedlichen Elektronengeschwindigkeiten nachgewiesen, dass die "relativistische" Masse (dynamische Masse) von schnellen Teilchen mit ihrer Geschwindigkeit zunimmt. Die dynamische Masse \(m_{\rm{rel}}\) ist also von ihrer Geschwindigkeit \(v\) abhängig. Es gilt \( m_\rm{rel} = m \left( v \right) \).
Bezeichnet man die Ruhemasse1 eines Teilchens mit \(m_0\), so lässt sich aus den Versuchen die folgende Beziehung für die relativistische Masse ableiten:
Relativistische Masse
Für die relativistische Masse eines Teilchens gilt:\[m_{\rm{rel}}=m(v) = \frac{m_0}{\sqrt{1 - \left(\frac{v}{c}\right)^2}}\]Dabei ist \(m(v)\) die geschwindigkeitsabhängige Masse (relativistische Masse), \(m_0\) die Ruhemasse und \(v\) die Teilchengeschwindigkeit.
1Die Ruhemasse \(m_0\) eines Teilchens wird von einem Beobachter festgestellt, der in Bezug auf das Teilchen in Ruhe ist und in einem Inertialsystem als ruhend beschrieben werden kann.
Relativistischer Impuls
Die Beziehung für den Impuls \(p\), die in der klassischen Mechanik den Ausdruck \(p=m\cdot v\) besitzt, wird in der speziellen Relativitätstheorie beibehalten. Allerdings setzt man für die Masse nun die relativistische Masse \(m_{\rm{rel}}\) ein.
Relativistischer Impuls
Für den relativistischen Impuls gilt:\[p = m_{\rm{rel}}\cdot v \Rightarrow p = \frac{m_0}{\sqrt{1 - \left(\frac{v}{c}\right)^2}} \cdot v\]
Aufgabe
Berechne, bei welcher Geschwindigkeit \(v\) die relativistische Masse \(m_{\rm{rel}}\) eines Teilchens dreimal so groß wie die Ruhemasse \(m_0\) ist.
Herleitung
Wenn du daran interessiert bist, wie sich obige Beziehung aus den Einsteinschen Postulaten ableiten lässt (wir wählen dazu ein einfaches Beispiel), so kannst du dir diese Herleitung hier ansehen.
Für die Herleitung der relativistischen Massenformel wird der völlig inelastische, zentrale Stoß zweier gleichartiger Teilchen in verschiedenen Inertialsystemen S und S' betrachtet. Wir gehen dabei von den folgenden Postulaten aus:
-
Die Masse der Teilchen ist geschwindigkeitsabhängig: \({m_{\rm{rel}}} = m\left( {\left| {\vec v} \right|} \right) = m\left( v \right)\)
-
Für den Impuls p gilt, ähnlich wie in der klassischen Physik: \(\vec p = m\left( v \right) \cdot \vec v\)
-
Die Erhaltung der Gesamtmasse (vgl. 1.) und des Gesamtimpulses (vgl. 2.) gilt in allen Inertialsystemen.
Zunächst wird der inelastische, zentrale Stoß der beiden gleichartigen Teilchen in deren Schwerpunktssystem (S'-System) betrachtet. Das Endprodukt des Stoßes muss in diesem System ruhen.
Anschließend wird der Vorgang von einem System S aus betrachtet, von dem aus gesehen sich das System S' mit der Geschwindigkeit \(v\) nach rechts bewegt. Von diesem System S aus betrachtet hat der rechte Stoßpartner die Geschwindigkeit Null, das Endprodukt des Stoßes bewegt sich mit der Geschwindigkeit \(v\) nach rechts.
Für die Geschwindigkeit \(u\) des linken Teilchens im S-System erhält man mit der Formel für die relativistische Geschwindigkeitsaddition\[u = \frac{{u' + v}}{{1 + \frac{{u' \cdot v}}{{{c^2}}}}}\]Mit \({u' = v}\) ergibt sich\[u = \frac{{2 \cdot v}}{{1 + \frac{{{v^2}}}{{{c^2}}}}}\quad (5)\]
Aus den Gleichungen \((3)\) bis \((5)\) lässt sich die relativistische Massenformel gewinnen: Löst man \((3)\) nach \(M(v)\) auf und setzt in \((4)\) ein, so erhält man\[m(u) \cdot u = \left( {m(u) + {m_0}} \right) \cdot v \Rightarrow m(u) = \frac{{{m_0}}}{{\frac{u}{v} - 1}}\quad (6)\]
Wenn du auch an der algebraischen Herleitung von (6) interessiert bist, so kannst du dir diese Herleitung hier ebenfalls einblenden.
Mit Hilfe von (5) kann man den Nenner des Bruches bei (6) durch u allein ausdrücken. Es gilt \[\frac{u}{v} - 1 = \sqrt {1 - {{\left( {\frac{u}{c}} \right)}^2}} \quad (7)\] Somit ergibt sich für die dynamische Masse ((7) in (6) einsetzen) \[m(u) = \frac{{{m_0}}}{{\sqrt {1 - {{\left( {\frac{u}{c}} \right)}^2}} }}\]
Zu zeigen ist \[\frac{u}{v} - 1 = \sqrt {1 - {{\left( {\frac{u}{c}} \right)}^2}} \] Mit Hilfe der Formel für die relativistische Geschwindigkeitsaddition \(u = \frac{{2 \cdot v}}{{1 + \frac{{{v^2}}}{{{c^2}}}}}\quad (5)\), kann der Nenner von \(m(u) = \frac{{{m_0}}}{{\frac{u}{v} - 1}}\quad (6)\) umgeschrieben werden. Aus \((5)\) ergibt sich \[u = \frac{{2 \cdot v}}{{1 + \frac{{{v^2}}}{{{c^2}}}}} \Leftrightarrow \left( {1 + \frac{{{v^2}}}{{{c^2}}}} \right) \cdot \frac{u}{v} = 2\,| \cdot \frac{u}{v} \Leftrightarrow \left( {1 + \frac{{{v^2}}}{{{c^2}}}} \right) \cdot \frac{{{u^2}}}{{{v^2}}} = 2 \cdot \frac{u}{v} \Leftrightarrow \frac{{{u^2}}}{{{v^2}}} + \frac{{{u^2}}}{{{c^2}}} = 2 \cdot \frac{u}{v}\] und weiter \[\frac{{{u^2}}}{{{v^2}}} - 2 \cdot \frac{u}{v} = - \frac{{{u^2}}}{{{c^2}}}\,\,| + 1 \Leftrightarrow \frac{{{u^2}}}{{{v^2}}} - 2 \cdot \frac{u}{v} + 1 = 1 - \frac{{{u^2}}}{{{c^2}}} \Leftrightarrow {\left( {\frac{u}{v} - 1} \right)^2} = 1 - \frac{{{u^2}}}{{{c^2}}}\] woraus sich schließlich ergibt \[\frac{u}{v} - 1 = \pm \sqrt {1 - \frac{{{u^2}}}{{{c^2}}}} \] Das Minuszeichen vor der Wurzel scheidet aus, da \(u > v\) und somit \(\frac{u}{v} - 1 > 0\) ist. Somit ist die Beziehung in der ersten Zeile hergeleitet.
Mit Hilfe von (5) kann man den Nenner des Bruches bei (6) durch \(u\) allein ausdrücken. Es gilt \[\frac{u}{v} - 1 = \sqrt {1 - {{\left( {\frac{u}{c}} \right)}^2}} \quad (7)\] Somit ergibt sich für die dynamische Masse ((7) in (6) einsetzen) \[m(u) = \frac{{{m_0}}}{{\sqrt {1 - {{\left( {\frac{u}{c}} \right)}^2}} }}\]