Von allen Paradoxa der Relativitätstheorie ist das sogenannte Uhren- oder Zwillingsparadoxon das berühmteste. Es handelt sich dabei um ein Gedankenexperiment, das bereits von Einstein (1911) formuliert wurde.
Aufgrund der Zeitdilatation, d.h. der Aussage "bewegte Uhren gehen langsamer", wird behauptet: Verbleibt von zwei gleichartigen Uhren eine in einem Inertialsystem in Ruhe, während man die zweite auf eine Reise mitnimmt und an deren Ende schließlich wieder an den Ort der ersten zurückbringt, so wird die zweite Uhr gegenüber der ersten nachgehen. In der Zwillingsversion desselben Gedankenversuchs bedeutet das: Geht einer von zwei Zwillingen auf eine "Raumfahrt", so ist er nach seiner Rückkehr zur Erde jünger als sein zu Hause gebliebener Zwillingsbruder (vgl. Abb. 1).
Ein Zahlenbeispiel
Zur Veranschaulichung betrachten wir ein einfaches Zahlenbeispiel, das von Darwin vorgeschlagen wurde:
An einem Neujahrstag verlässt Astronaut Max seinen Zwillingsbruder Sepp in einem Raumschiff, das mit \(v=0{,}8\cdot c\) fährt. Nach zehn Jahren, gemessen von der Erde aus, kehrt er um und fährt mit gleicher Geschwindigkeit zurück. Dort trifft er nach einer Gesamtreisezeit von zwanzig Jahren (Erdzeit) wieder ein.
Für die Borduhren hat die Hinreise wegen der Zeitdilatation jedoch nur\[\sqrt {1 - {{\left( {\frac{v}{c}} \right)}^2}} \cdot 10\,\text{Jahre} = \sqrt {1 - {{\left( {0,80} \right)}^2}} \cdot 10\,\text{Jahre}= 6\,\text{Jahre}\]gedauert, ebenso wie die Rückreise (Der Effekt der Zeitdilatation ist von der Bewegungsrichtung unabhängig; die hergeleiteten Formeln gelten ebenso für eine negative Geschwindigkeit \(v\)). Max war also insgesamt nur 12 Jahre nach Bordzeit unterwegs. Nach der Rückkehr ist Max um 8 Jahre jünger als Sepp.
Wege jährlich ausgesandter Lichtsignale
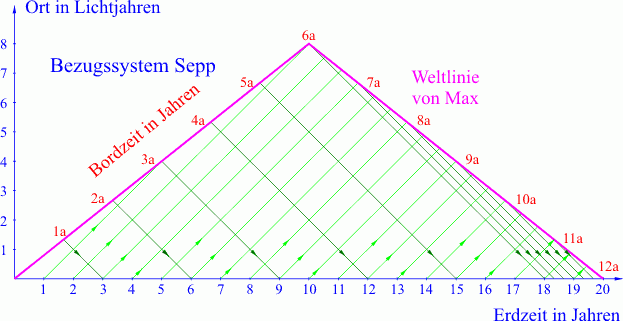
Der Zusammenhang zwischen den Zeitmessungen auf der Erde bzw. an Bord wird in einem Zeit-Ort-Diagramm noch deutlicher. Dabei wollen wir zusätzlich annehmen, dass die Brüder einander jeweils zum Neujahrstag (jeder nach seiner Uhr) per Funk Glückwünsche schicken (vgl. Abb. 2).
Über die Zahl der Signale sind sich die Zwillinge einig:
- Sepp, der Erdbewohner, sendet neunzehn und Max der Astronaut empfängt neunzehn Signale.
- Max sendet elf und Sepp empfängt elf Signale.
Beide empfangen die Signale mit der jeweils korrekten Dopplerverschiebung (vgl. Minkowski-Diagramme).
Solange sich die Uhren voneinander fortbewegen, treffen die Signale in Zeitabständen\[k(v) \cdot 1\,\text{Jahr} = \sqrt {\frac{{c + v}}{{c - v}}} \cdot 1\,\text{Jahr} = \sqrt {\frac{{1,8 \cdot c}}{{0,2 \cdot c}}} \cdot 1\,\text{Jahr} = 3\,\text{Jahren}\]ein.
Sobald sich die Uhren einander nähern, ist die Empfangsperiode\[k( - v) \cdot 1\,\text{Jahr} = \sqrt {\frac{{c - v}}{{c + v}}} \cdot 1\,\text{Jahr} = \sqrt {\frac{{0,2 \cdot c}}{{1,8 \cdot c}}} \cdot 1\,\text{Jahr}=\frac{1}{3}\,\text{Jahr}\]