Quantenobjekt Photon

Versuche

\(h\)-Bestimmung mit der Gegenfeldmethode

Vorlesen

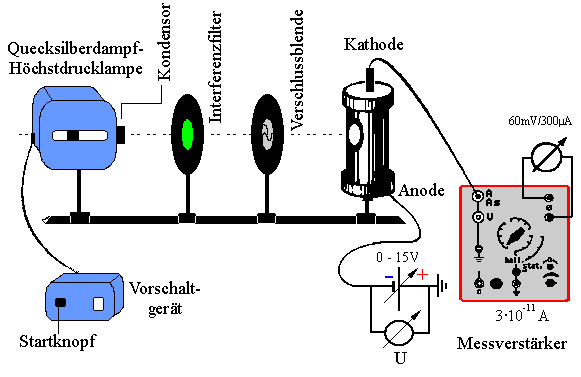
Aufbau und Durchführung

Die Kathode der Vakuumfotozelle wird mit intensivem monochromatischem Licht bestrahlt, das man aus einer Quecksilberhöchstdrucklampe mit geeignetem Interferenzfiltern erhält.
Es wird der Photostrom mittels stromempfindlichen Messverstärker abgelesen und die Gegenspannung langsam so lange hoch geregelt, bis der Photostrom Null ist.
Diese maximale Gegenspannung ist abhängig von der Frequenz, aber unabhängig von der Intensität des eingestrahlten Lichtes.

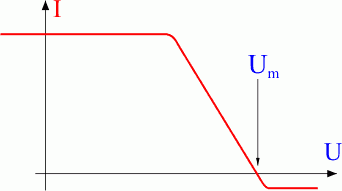
\(U\)-\(I\)-Diagramm (Kennlinie)

**Abb. 4** \(U\)-\(I\)-Diagramm im Versuch

Qualitativ sieht der Anodenstrom in Abhängigkeit von der Gegenspannung so wie in Abb. 4 aus. Der kleine negative Strom ist bei höheren Frequenzen bedingt durch Photoelektronen, die von reflektierten Strahlen am Anodenring ausgelöst werden.

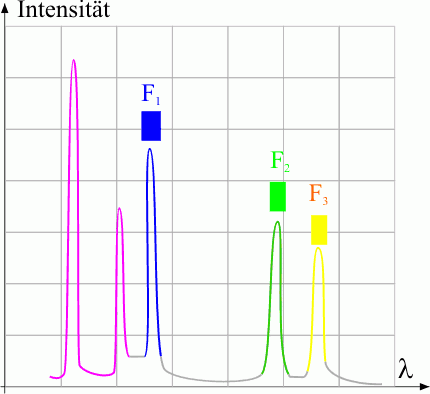
Filter

Als Filter verwendet man Interferenzfilter, die nur das Licht je einer der typischen Quecksilberlinien durchlässt.

Es sind dies:

ein Gelbfilter F₃ für \(578\,\rm{nm}\),
ein Grünfilter F₂ für \(546\,\rm{nm}\) und
ein Blaufilter F₁ für \(436\,\rm{nm}\)

In Abb. 5 ist das Spektrum der Quecksilberdampflampe mit den drei Filtern im sichtbaren Bereich des Spektrums dargestellt. Die beiden UV-Linien werden nicht verwendet.

Beobachtung

Wir erhalten folgende Messwerte:

**Tab. 1** Messwerte
Farbe	gelb	grün	blau
Wellenlänge \(\lambda\;\rm{in}\;\rm{nm}\)	\(578\)	\(546\)	\(436\)
Frequenz \(f\;\rm{in}\;10^{14}\,\rm{Hz}\)	\(5{,}19\)	\(5{,}49\)	\(6{,}88\)
Spannung \(U_{\rm{m}}\;\rm{in}\;\rm{V}\)	\(0{,}75\)	\(0{,}85\)	\(1{,}40\)
Maximale kinetische Energie \(E_{\rm{kin,e}}\) der Photoelektronen \(\rm{in}\;\rm{eV}\)	\(0{,}75\)	\(0{,}85\)	\(1{,}40\)

Auswertung

**Abb. 6** \(f\)-\(E_{\rm{kin,e}}\)-Diagramm

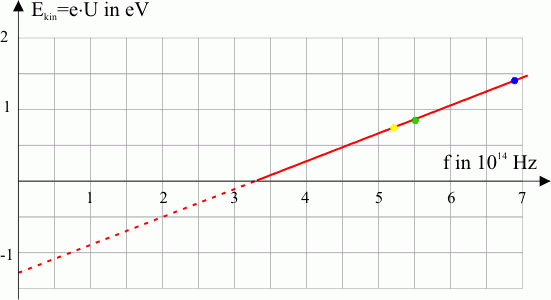
Man trägt die Ergebnisse für die drei Teilversuche in ein \(f\)-\(E_{\rm{kin,e}}\)-Diagramm ein.
Die Messpunkte liegen nahezu auf einer Geraden deren Steigung das PLANCKsche Wirkungsquantum \(h\) ist und deren Energie-Achsenabschnitt die Austrittsarbeit \(W_{\rm{A}}\) des Kathodenmaterials ist.

Hinweis: In dem Frequenzbereich, in dem bei dem verwendeten Kathodenmaterial kein Photoeffekt auftritt, sollte die Gerade gestrichelt werden.

Aufgabe

Bestimme mit Hilfe des \(f\)-\(E_{\rm{kin,e}}\)-Diagramms in Abb. 6

die Austrittsarbeit \(W_{\rm{A}}\)
die Grenzfrequenz \(f_{\rm{G}}\) (das ist die Frequenz, ab der der Photoeffekt auftritt) und
das PLANCKsche Wirkungsquantum \(h\).

Das PLANCKsche Wirkungsquantum - eine universelle Konstante

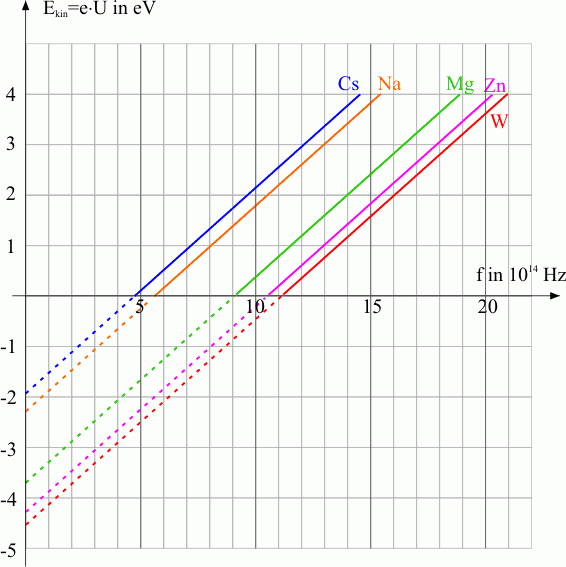
**Abb. 8** Grenzfrequenz und Austrittsarbeit bei verschiedenen Kathodenmaterialien

Führt man die Gegenfeldmethode mit verschiedenen Kathodenmaterialien durch, so zeigen sich z.B. für Cäsium (Cs), Natrium (Na), Magnesium (Mg), Zink (Zn) und Wolfram (W) die in Abb. 8 dargestellten Versuchsergebnisse.

Aus dem Diagramm erkennst du:

Die Grenzfrequenz \(f_{\rm{G}}\) und die Austrittsarbeit \(W_{\rm{A}}\) hängen vom Kathodenmaterial ab.
Die Steigung der Geraden und damit das PLANCKsche Wirkungsquantum \(h\) ist materialunabhängig. Die PLANCKsche Konstante ist eine universelle Naturkonstante.

Drucken