Das Photonenbild löst Verständnisprobleme, die bei klassischer Betrachtung des Photoeffekts auftreten
Mit dem Photonenbild des Lichts können die mit dem klassischen Wellenmodell des Lichts schwer verständlichen Versuchsergebnisse, welche beim Photoeffekt zu beobachten sind, zwanglos erklärt werden.
Problem 1: Existenz einer oberen Grenzwellenlänge
Bei der Bestrahlung einer Zinkplatte mit dem Licht einer Quecksilberdampflampe stellt man fest, dass bei negativer Vorladung der Zinkplatte eine Entladung und somit der Photoeffekt stattfindet.
Filtert man nun den sehr kurzwelligen UV-Anteil der Hg-Lampe mittels einer Glasplatte heraus, so findet kein Photoeffekt statt, selbst dann nicht, wenn die Bestrahlungsintensität der Zinkplatte durch Annäherung der Hg-Lampe um ein Vielfaches gesteigert wird.
Ob überhaupt Photoeffekt an einer bestimmten Oberfläche stattfindet oder nicht hängt also von der Wellenlänge (bzw. Frequenz) der auftreffenden Strahlung ab.
Beim Überschreiten eines bestimmten Grenzwertes der Wellenlänge (obere Grenzwellenlänge λG) zeigt sich auch bei gesteigerter Intensität der Strahlung kein Photoeffekt.
Höhere Intensität führt nicht zu einem Strom
Klassisch könnte man sich jedoch vorstellen, dass die Elektronen durch Licht höherer Intensität (→ Welle hat höhere Amplitude) aus der Materieschicht "herausgerissen" werden und so bei beliebiger Wellenlänge ein Strom zu beobachten sein sollte, wenn nur die Intensität des Lichts groß genug ist. Dies lässt sich jedoch experimentell widerlegen. Daher sind Zweifel an der Wellentheorie des Lichts berechtigt.
Erklärung im Photonenbild
Wenn die Photonenenergie kleiner oder gleich der Austrittsarbeit ist, kommt es zu keiner Auslösung von Elektronen. \[h \cdot f \leq W_A \Rightarrow f \leq \frac{W_A}{h} \Rightarrow \frac{c}{\lambda} \leq \frac{W_A}{h}\] \[\lambda \geq \frac{h\cdot c}{W_A} \underrightarrow{\small{\text{ Grenzwellenlänge }} } \lambda_G = \frac{h \cdot c}{W_A}\]
Problem 2: Trägheitsloses Einsetzen
Bei der Bestrahlung einer gasgefüllten Photozelle, an der eine "Saugspannung" liegt, mit einem Stroboskop stellt man fest, dass der Photostrom fast augenblicklich auf die Einstrahlung des Lichts folgt.
Würde sich das von der Lichtquelle ausgesandte Licht "gleichmäßig" über den Raum verteilen, wie es die Wellentheorie des Lichts verlangt, so wäre ein sofortiges Einsetzen des Photoeffekts nicht verständlich, wie es die folgende - etwas waghalsige - Abschätzung und die nebenstehende Animation für die Bestrahlung einer Metallplatte mit einer Hg-Lampe zeigt.
Abschätzung der Ablösezeit für ein Elektron aus einer Zinkplatte
Es werde angenommen, dass die verwendete Quecksilberdampflampe eine elektrische Leistung von \(P=200\,\rm{W}\) aufnimmt. Erfahrungsgemäß beträgt die Lichtleistung der Lampe dann maximal 10% der aufgenommenen elektrischen Leistung, also \(P=20\,\rm{W}\). Nach der klassischen Wellenvorstellung vom Licht müsste sich die Lichtleistung der als punktförmig angenommenen Lichtquelle gleichmäßig im Raum verteilen. Die in der Entfernung \(r=1{,}0\,\rm{m}\) von der Quelle angeordnete Zinkplatte erhält dann eine "Flächen-Lichtleistung" von \[\frac{{{P_{licht}}}}{A} = \frac{{{P_{licht}}}}{{4 \cdot \pi \cdot {r^2}}} \Rightarrow \frac{{{P_{licht}}}}{A} = \frac{{20}}{{4 \cdot \pi \cdot 1{,}0^2}}\rm{\frac{W}{{{m^2}}}} \approx 1{,}6\rm{\frac{W}{{m^2}}}\]
Geht man weiterhin davon aus, dass sich diese Flächenleistung auch gleichmäßig auf die in der Oberfläche der Metallplatte sitzenden Zinkatome mit einer "atomaren Fläche" von\[A' = r_{atom}^2 \cdot \pi \Rightarrow A' = {\left( {1,0 \cdot {{10}^{ - 10}}} \right)^2} \cdot \pi \,\rm{m^2} \approx 3 \cdot {10^{ - 20}}\,\rm{m^2}\]verteilt und berücksichtigt man, dass etwa 90% des Lichtes an der Oberfläche reflektiert wird, so kann eine Zinkatom in etwa die Leistung \(P{'_{aufg}}\) aufnehmen:\[P{'_{aufg}} = 0{,}10 \cdot \frac{{{P_{licht}}}}{A} \cdot A' \Rightarrow P{'_{aufg}} = 0{,}10 \cdot 1{,}6 \cdot 3 \cdot {10^{ - 20}}\,\rm{W} \approx 5 \cdot {10^{ - 21}}\,\rm{W}\]
Hinweis: Die tatsächliche Leistung, welche nun für den Photoeffekt am Zn-Atom zur Verfügung steht, dürfte noch deutlich geringer sein, da nur der UV-Anteil des Lichts zu betrachten ist.
Aus Experimenten weiß man, dass zum Ablösen eines Elektrons aus der Metalloberfläche eine Ablösearbeit von ca. \(W_{\rm{A}}=4\,\rm{eV}\approx 6\cdot 10^{-19}\,\rm{J}\) aufzubringen ist. Unter der gewagten Annahme, dass jedes Atom in der Oberfläche den ihm zustehenden Energiebetrag von \(P{'_{aufg}}\cdot\Delta t\) speichern könnte, bis es die Ablösearbeit "angespart" hat, so verginge eine Zeit von\[\Delta t = \frac{{{W_A}}}{{P{'_{aufg}}}} \Rightarrow \Delta t = \frac{{6 \cdot {{10}^{ - 19}}}}{{5 \cdot {{10}^{ - 21}}}}\,\rm{\frac{J}{W}} \approx 1 \cdot {10^2}\,\rm{s}\]bis ein Elektron ausgelöst würde. Tatsächlich setzt der Photoeffekt unmittelbar bei Bestrahlung ein.
Erklärung im Photonenbild
Die Energie der elektromagnetischen Strahlung ist nicht kontinuierlich über den Raum, sondern auf die "Energiepakete Photonen" verteilt. Ein Photon löst (bei entsprechenden Voraussetzungen) in einem "Elementarakt" ein Elektron aus der Oberfläche des Körpers aus.
Problem 3: Unabhängigkeit der kinetischen Energie der Photoelektronen von der Lichtintensität
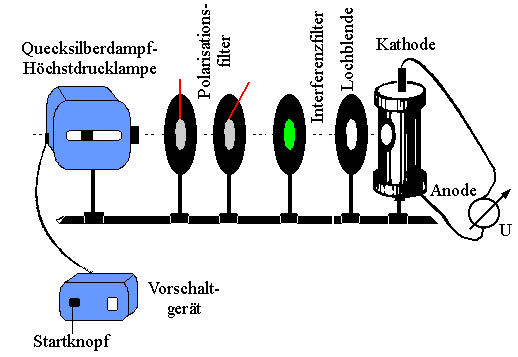
Mit dem folgenden Versuch kann gezeigt werden, dass die kinetische Energie der bei einer bestimmten Lichtfrequenz ausgelösten Photoelektronen unabhängig von der Lichtintensität ist.
Mit einer Lochblende wird dafür gesorgt, dass das Licht einer Quecksilberdampflampe (Hg-Lampe) hauptsächlich auf die Kathode und nicht auf die ringförmige Anode der Photozelle trifft. Das Material der Photokathode ist so beschaffen, dass der Photoeffekt - im Gegensatz zu einer Zinkplatte - schon bei sichtbarem Licht auftritt.
In den Strahlengang wird ein Interferenzfilter gebracht, welches z.B. nur grünes Licht auf die Photokathode treffen lässt.
Abhängig von der Frequenz des eingestrahlten Lichts bildet sich an der Photozelle eine bestimmte Spannung aus (der Minuspol ist dabei die Anode, der Pluspol die Kathode), die mit einem extrem hochohmigen Voltmeter (Verstärker plus Anzeigegerät) festgestellt wird.Aus der Spannung lässt sich die kinetische Energie der ausgelösten Elektronen bestimmen (vgl. unten).
Nun bringt man in den Strahlengang zwei Polarisationsfilter. Durch sie kann die Intensität des auf die Photokathode treffenden Lichtes in einem weiten Bereich variiert werden:
Stimmen die Zeigerstellungen für die Durchlassrichtung beider Filter überein, so gelangt möglichst viel Licht auf die Photokathode.
Bilden die Zeiger miteinander einen Winkel von 90°, so gelangt kein Licht auf die Photokathode.
Es zeigt sich, dass die gemessene Spannung und somit die kinetische Energie der Elektronen weitgehend unabhängig von der eingestrahlten Lichtintensität ist.
Zusammenhang zwischen der kinetischen Energie \(E_{\rm{kin,Elektronen}}\) der ausgelösten Photoelektronen und der Spannung \(U\)
Solange noch kein Licht auf die Kathode trifft, sind Kathode und Anode neutral, die Spannung zwischen diesen beiden Elektroden ist Null.
Beim Auftreffen von Photonen mit ausreichender Energie \(E_{\rm{Photon}}>W_{\rm{A}}\) lösen sich die ersten Elektronen aus der Kathode. Abhängig von der Photonenenergie und der Ablösearbeit des Kathodenmaterials besitzen die ausgelösten Elektronen eine bestimmte Anfangsgeschwindigkeit und damit kinetische Energie. In der Abb. 8 ist dies durch einen Pfeil beim ersten Elektron symbolisiert.
Die ersten Elektronen werden von der Anode kaum abgestoßen, da diese noch fast neutral ist. Die nachfolgenden Elektronen (mit gleicher kinetischer Anfangsenergie wie die ersten Elektronen) werden von der nun zunehmend negativen Anode abgestoßen, sie erreichen diese aber noch.
Aufgrund der Ladungstrennung - die Kathode wird immer stärker positiv, die Anode wird immer stärker negativ geladen - wächst die Spannung zwischen Anode und Kathode.
Schließlich ist die Abstoßung der später ausgelösten Elektronen durch die Anode so stark, dass diese Elektronen nicht mehr zur Anode gelangen können. Die Ladungstrennung hat eine Sättigung und damit die Spannung einen stabilen Endwert erreicht, der ein Maß für die kinetische Energie der Elektronen ist. Es gilt: \[{E_{\rm{kin,Elektronen}}} = e \cdot U\]
Hinweis: Kathoden in Fotozellen sind meist aus Materialien bei denen nur eine geringe Austrittsarbeit notwenig ist, z.B. aus Caesium mit einer Austrittsarbeit zwischen 1,7 und 2,14 eV. Hier reicht daher schon gelbes Licht, um Elektronen auszulösen. Bei der Zinkplatte aus dem ersten Versuch (vgl. Abb. 1) beträgt die Ablösearbeit 4,34 eV, sodass sichtbares Licht keine Elektronen aus Zink auslösen kann.
Hinweis: Stellt sich an der Photozelle z.B. die Spannung 1,0 V ein, so war die maximale kinetische Energie der Photoelektronen \( E_\text{kin} = e \cdot U = 1{,}60 \cdot 10^{-19}\, \mathrm{A \cdot s} \cdot 1{,}0\, \mathrm{V} = 1{,}60 \cdot 10^{-19}\, \mathrm{J} = 1\, \mathrm{eV} \).
Erklärung im Photonenbild
Höhere Lichtintensität bedeutet im Photonenbild eine höhere Photonendichte. In der Bestimmungsgleichung \(h \cdot f = W_{\rm{A}}+E_{\rm{kin,el}}\) für die kinetische Energie der Elektronen kommt die Photonendichte bzw. die Intensität \(J\) nicht vor.


