Arthur Holly COMPTON (1892 - 1962) bestrahlte um 1922 einen Streukörper mit monochromatischer RÖNTGEN-Strahlung der Wellenlänge \(\lambda\). Er stellte fest, dass Anteile der Streustrahlung je nach Streuwinkel eine höhere Wellenlänge \(\lambda'\) aufweisen. Im Photonenbild bedeutet dies, dass Photonen der Streustrahlung eine kleinere Energie haben als die Photonen der ursprünglichen Strahlung.
COMPTON erklärte seine Versuchsergebnisse durch elastische Stöße der ankommenden Photonen mit quasifreien Elektronen der äußeren Atomhülle, bei denen die Photonen Energie verlieren und die Elektronen kinetische Energie gewinnen.
Bei einem elastischen Stoß mit fest gebundenen inneren Elektronen verliert das Photon nahezu keine Energie, das innere Elektron bleibt gebunden. Daher enthält die Streustrahlung auch einen Anteil, dessen Wellenlänge mit der Wellenlänge der ursprünglichen Strahlung übereinstimmt.
Aufbau und Durchführung
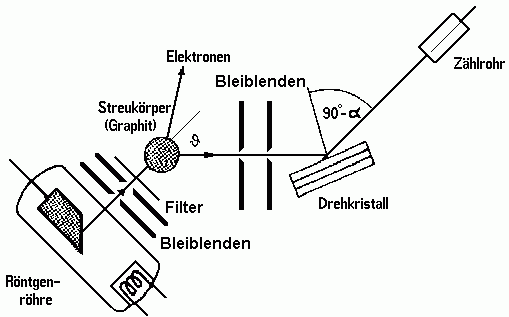
COMPTON verwendete 1923 die in Abb. 2 skizzierte Anordnung, bei der er einen fein ausgeblendeten Röntgenstrahl auf einen Streukörper treffen ließ und die gestreute Strahlung mittels einer BRAGGschen-Drehkristallanordnung auf ihre Wellenlänge untersuchte.
Beobachtung
- In der Streustrahlung tritt neben der Wellenlänge \(\lambda\) der ursprünglichen RÖNTGEN-Strahlung noch die größere Wellenlänge \(\lambda '\)auf.
- Die Wellenlängendifferenz \(\lambda '- \lambda\) der Peaks wird mit größerer Winkelweite \(\vartheta\) größer (siehe Abb. 3).
- Je größer die Winkelweite \(\vartheta\), desto geringer wird der verlustfrei reflektierte Anteil mit Wellenlänge \(\lambda\) und um so größer wird der Anteil mit der größeren Wellenlänge \(\lambda '\) (siehe Abb. 3).
- Ändert man das Material des Streukörpers bei gleichbleibender Strahlung, so bleibt der Wellenlängenunterschied \(\lambda ' - \lambda\) gleich (siehe Abb. 4).
- Der Anteil verlustfrei reflektierter Strahlung mit Wellenlänge \(\lambda\) wird um so größer, je höher die Ordnungszahl des Elements ist, welches als Streukörper verwendet wird.
Erklärung des COMPTON-Effekts
Die Versuchsergebnisse des COMPTON-Effekts können als vollständig elastischer Stoß eines Photons mit einem zunächst ruhenden Elektron gedeutet werden. Das Photon gibt dabei einen Teil seiner Energie und seines Impulses an das Elektron ab.
Für die Wellenlänge \(\lambda'\) der gestreuten Strahlung in Abhängigkeit von der Wellenlänge \(\lambda\) der einfallenden Strahlung und der Weite \(\vartheta\) des Streuwinkels ergibt sich durch theoretische Überlegungen (siehe unten) der Zusammenhang\[\lambda' = \lambda + \frac{h}{m_{\rm{0,e}} \cdot c} \cdot \left(1-\cos\left(\vartheta\right) \right)\]der die experimentellen Ergebnisse exakt widergibt. Mit \(\Delta\lambda = \lambda' - \lambda\) und der sogenannten COMPTON-Wellenlänge \(\lambda_{\rm{C}} = \frac{h}{m_{\rm{0,e}}\cdot c} = 2{,}4263 \cdot 10^{-12}\,\rm{m}\) (5 gültige Ziffern) wird dieser Zusammenhang oft beschrieben durch die Gleichung\[\Delta\lambda = \lambda_{\rm{C}} \cdot \left(1-\cos\left(\vartheta\right)\right) \]
Merkregel
Ein Photon mit der COMPTON-Wellenlänge \({\lambda _{\rm{C}}}\) hat wegen\[{E_{{\rm{Ph}}{\rm{,}}{\lambda _{\rm{C}}}}} = h \cdot \frac{c}{{{\lambda _{\rm{C}}}}} = h \cdot \frac{c}{{\frac{h}{{{m_{0,e}} \cdot c}}}} = {m_{0,e}} \cdot {c^2} = {E_{0,e}}\]die Energie, die der Ruhemasse des Elektrons entspricht.
Um nicht zu viele Indizes zu verwenden sollen für die Herleitung folgende Bezeichnungen verwendet werden:
| Objekt | Energie | Impuls | Wellenlänge |
|---|---|---|---|
| Photon vor dem Stoß | \(E\) | \(\vec{p}\) | \(\lambda\) |
| Photon nach dem Stoß | \(E'\) | \(\vec{p}'\) | \(\lambda'\) |
| Elektron vor dem Stoß | \(E_0\) | \(0\) | |
| Elektron nach dem Stoß | \(E_{\rm{e}}\) | \(\vec {p}'_{\rm{e}}\) |
Es gelten die folgenden physikalischen Gesetze:
- Energieerhaltungssatz:\[E + E_0 = E' + E_{\rm{e}} \quad (1) \]
- Impulserhaltungssatz (vektoriell): \[\vec{p} = \vec{p}' + \vec{p}'_{\rm{e}} \quad (2')\]Dies führt über den Kosinussatz zur Gleichung\[{{p'}_e}^2 = p^2 + {p'}^2 -2 \cdot p \cdot p' \cdot \cos(\vartheta) \quad (2)\]
- Die Energie-Impuls-Beziehungen aus der speziellen Relativitätstheorie\[ \text{für das Elektron: } E_e^2 = E_0^2 + c^2 \cdot {p'}_e^2 \quad \rm{(3a)} \]
\[ \text{ für das Photon vorher: } E = p \cdot c \quad \rm{(3b)}\]
\[ \text{für das Photon nachher: } E' = p' \cdot c \quad \rm{(3c)}\]
Gesucht ist nun die Energie oder der Impuls oder die Wellenlänge des gestreuten Photons in Abhängigkeit von den Daten des ungestreuten Photons und des Winkels \(\vartheta\). Hierzu setzt man die einfacheren Gleichungen \((1)\) und \((3)\) in die kompliziertere Gleichung \((2)\) ein.
\[E + E_0 = E' + E_{\rm{e}} \Leftrightarrow E_{\rm{e}} = E + E_0 – E' \quad (1') \]
(3a) \({p'}_e^2 = \frac{E_e^2 – E_0^2}{c^2} = \frac{(E+ E_0-E’)^2- E_0^2}{c^2} \)
(3b) \(p = \frac{E}{c}\)
(3c) \(p' = \frac{E'}{c}\)
in \((2)\) ergibt\[\frac{(E + E_0 – E')^2-E_0^2}{c^2} = \frac{E^2}{c^2} + \frac{E'^2}{c^2} – 2 \frac{E\cdot E'}{c^2} \cos \left(\vartheta\right)\qquad |\cdot c^2\]Nun muss man noch vereinfachen:\[E^2 + E_0^2 + E'^2 + 2E\cdot E_0 – 2E\cdot E' – 2 E' \cdot E_0 – E_0^2 = E^2 + E'^2-2E \cdot E' \cos \left(\vartheta\right)\]Damit ergibt sich\[2E \cdot E_0 – 2E \cdot E' – 2E'\cdot E_0 = -2E\cdot E' \cos \left(\vartheta\right)\qquad | \cdot \frac{1}{2 \cdot E \cdot E'\cdot E_0}\]und weiter\[\frac{1}{E'}-\frac{1}{E_0}-\frac{1}{E} = \frac{-\cos \left(\vartheta\right)}{E_0}\]Durch Einsetzen der Energieformel des Photons ergibt sich\[\frac{\lambda'}{h \cdot c} - \frac{\lambda}{h \cdot c} = \frac{1}{E_0}\cdot (1-\cos \left(\vartheta\right) ) \qquad| \cdot (h\cdot c)\]und schließlich\[\lambda'-\lambda = \frac{h\cdot c}{m_{0,e}\cdot c^2}(1-\cos\left(\vartheta\right))\]Mit der sogenannten COMPTON-Wellenlänge \[\lambda_c = \frac{h}{m_{0,e}\cdot c} = 2,42 \cdot 10^{-12}m\]schließlich\[ {\Delta\lambda = \lambda_c(1-\cos\left(\vartheta\right))} \]
Hinweis zum Lösen von Aufgaben zum COMPTON-Effekt
Die obige Gleichung beschreibt den Zusammenhang zwischen den Wellenlängen \(\lambda\) und \(\lambda'\) von einfallender und gestreuter Strahlung. Oft ist in Aufgabenstellungen zum COMPTON-Effekt aber die Quantenenergie \({E}_{{\rm{Ph}}}\) oder die Frequenz \(f\) der einfallenden Strahlung gegeben oder aber die Quantenenergie \(E'_{{\rm{Ph}}}\) oder die Frequenz \(f'\) der gestreuten Strahlung gesucht. Für diese Fälle musst du nach dem folgenden Schema vorgehen.\[\begin{array}{*{20}{c}}{{E_{{\rm{Ph}}}}}& \to &f& \to &\lambda & \to &{\lambda '}& \to &{f'}& \to &{{E'_{{\rm{Ph}}}}}\\{}&{f = \frac{{{E_{{\rm{Ph}}}}}}{h}}&{}&{\lambda = \frac{c}{f}}&{}&{\lambda ' = \lambda + {\lambda _{\rm{C}}} \cdot \left( {1 - \cos \left( \vartheta \right)} \right)}&{}&{f' = \frac{c}{{\lambda '}}}&{}&{{E'_{{\rm{Ph}}}} = h \cdot f'}&{}\end{array}\]