Der erste Nachweis des Wellencharakters von Elektronen gelang 1927 Clinton Joseph DAVISSON (1881-1958) und Lester Halbert GERMER (1896-1971) als Zufallsfund bei Experimenten zur Reflexion von Elektronen an einem Nickelkristall.
Das Experiment ist als das DAVISSON-GERMER-Experiment in die Geschichte eingegangen.
Aufbau und Durchführung
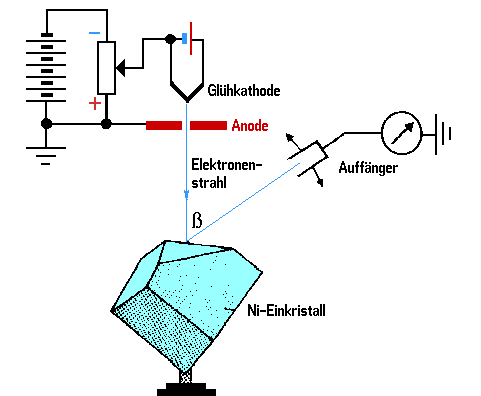
Im Versuch von DAVISSON und GERMER werden Elektronen senkrecht auf die Oberfläche eines Nickel-Einkristalls geschossen und die Intensität der reflektierten Elektronen als Funktion der Weite \(\beta\) des Streuwinkels gemessen.
Die Intensität der reflektierten Elektronen wird aus der Stärke des Stroms bestimmt, der vom Auffänger (FARADAY-Becher) zur Erde abfließt.
Beobachtung
Zur Überraschung der Experimentatoren ergaben sich keine "glatten" Kurven, sondern - abhängig vom Streuwinkel und der Beschleunigungsspannung - ausgeprägte Maxima. In den folgenden Bildern sind Polardiagramme der Intensität der reflektierten Elektronen dargestellt.
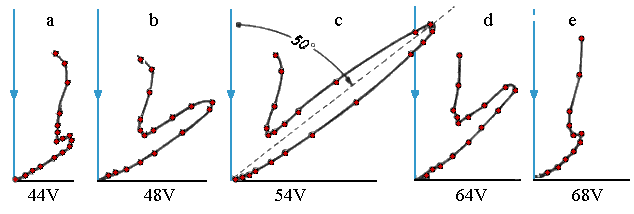
Man sieht, dass bei einer Beschleunigungsspannung von \(54\,\rm{V}\) ein besonders ausgeprägtes Maximum unter dem Winkel von \(\beta = 50^\circ\) auftritt. Man vermutete nun, dass es sich bei den Maxima - ähnlich wie bei der RÖNTGEN-Strahlung - um Beugungserscheinungen am Raumgitter des Kristalls handelt, welche schließlich zu Interferenzerscheinungen führen. Zum Verständnis war es also notwendig, die Elektronen als Materiewellen aufzufassen.
Auswertung
Mit Hilfe einer Detailbetrachtung kann gezeigt werden, dass die Versuchsergebnisse von DAVISSON und GERMER den Zusammenhang zwischen Materiewellenlänge und Impuls, den de BROGLIE in seiner Promotionsarbeit formulierte, bestätigen. Wir beschränken uns dabei auf das auffälligste Ergebnis, dass bei einer Beschleunigungsspannung von \(54\,\rm{V}\) unter dem Winkel der Weite \(\beta = 50^\circ \) ein deutliches Maximum auftritt.
Berechnung der Materiewellenlänge nach de BROGLIE
Die Elektronen besitzen die kinetische Energie von \(54\,\rm{eV}\). Bei diesen geringen Energien ist die nichtrelativistische Energie-Impuls-Beziehung anwendbar:\[E_{\rm{kin,e}} = \frac{{{m_{{\rm{0,e}}}} \cdot {v^2}}}{2} = \frac{{{m_{{\rm{0,e}}}}^2 \cdot {v^2}}}{{2 \cdot {m_{{\rm{0,e}}}}}} = \frac{p^2}{2 \cdot m_{\rm{0,e}}} \Rightarrow p = \sqrt {2 \cdot m_{\rm{0,e}} \cdot E_{\rm{kin,e}}} \]Einsetzen der gegebenen Werte liefert\[p = \sqrt {2 \cdot 9{,}11 \cdot 10^{-31}\,\rm{kg} \cdot 54 \cdot 1{,}60 \cdot 10^{-19}\,\rm{V}} = 3{,}97 \cdot 10^{-24}\,\rm{N\,s}\]Mit dem Ansatz von de BROGLIE folgt dann für die Materiewellenlänge\[\lambda _{\rm{dB}} = \frac{h}{p} \Rightarrow \lambda _{\rm{dB}} = \frac{6{,}63 \cdot 10^{-34}\,\rm{J\,s}}{3{,}97 \cdot 10^{-24}\,\rm{N\,s}} = 1{,}67 \cdot 10^{-10}\,\rm{m}\]
Berechnung der Wellenlänge aus den Messergebnissen mit Hilfe der Beziehung von BRAGG
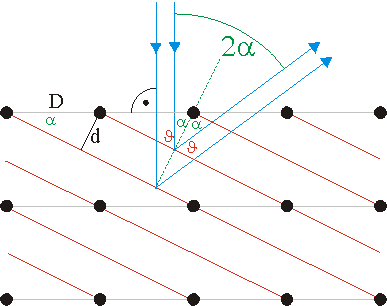
Durch RÖNTGEN-Strukturanalyse wurde für den Netzebenenabstand \(D = 2{,}15 \cdot 10^{-10}\,\rm{m}\) festgestellt. Für die von DAVISSON und GERMER beobachtete Interferenz sind die Netzebenen mit dem Abstand \(d\) relevant. Für diese gilt\[d = D \cdot \sin \left( \alpha \right) \Rightarrow d = 2{,}15 \cdot 10^{-10}\,\rm{m} \cdot \sin \left( {25^\circ } \right) = 9{,}09 \cdot 10^{-11}\,\rm{m}\]Zur Wellenlängenbestimmung durch den Interferenzversuch wird die BRAGG-Beziehung verwendet: Die Weite \(\beta \) des Ablenkwinkels ist gleich der Winkelweite \(2 \cdot \alpha \). Aus der Winkelweite \(\alpha \) kann nun leicht die Weite \(\vartheta \) des Glanzwinkels und damit die Wellenlänge \(\lambda \) bestimmt werden:\[\lambda = 2 \cdot d \cdot \sin \left( \vartheta \right) = 2 \cdot d \cdot \sin \left( {90^\circ - \alpha } \right)\]Einsetzen der gegebenen Werte liefert\[\lambda = 2 \cdot 9{,}09 \cdot 10^{-11}\,\rm{m} \cdot \sin \left( {90^\circ - 25^\circ } \right) = 1{,}65 \cdot 10^{-10}\,\rm{m}\]
Ergebnis
Die Auswertung zeigt, dass die nach de BROGLIE und die durch den Interferenzversuch nach BRAGG bestimmten Wellenlängen recht gut übereinstimmen. Insofern erbrachte der Versuch von DAVISSON und GERMER eine Bestätigung der Hypothese von de BROGLIE.



