In seiner berühmten Arbeit, die 1927 veröffentlicht wurde, gelangte Werner HEISENBERG (1901 - 1976) nach Überlegungen, die an der Schule in der Regel nicht nachvollzogen werden können, zu folgender Feststellung:
Unbestimmtheitsrelation
Ort und Impuls eines Teilchens können prinzipiell nicht gleichzeitig beliebig genau bestimmt werden. Mit anderen Worten: Eine gleichzeitige Bestimmung von Ort und Impuls eines Teilchens ist nur möglich, wenn für beide Größen eine Unbestimmtheit in Kauf genommen wird. Dabei gilt stets die Ungleichung: \[\Delta x \cdot \Delta {p_x} \ge \frac{h}{{4\pi }}\]Dabei ist \(\Delta x\) die Unbestimmtheit in der Angabe des Ortes \(x\), \(\Delta {p_x}\) die gleichzeitig vorhandene Unbestimmtheit in der Angabe des Impulses \({p_x}\) und \(h\) das plancksche Wirkungsquantum.
Anmerkungen:
- In der Literatur finden sich für die rechte Seite dieser Ungleichung verschiedene Werte. Wesentlich ist dabei die Größenordnung!
- Ähnliche Unbestimmtheitsrelationen gibt es auch für die anderen Raumrichtungen, d.h. \(\Delta y \cdot \Delta {p_y} \ge \frac{h}{{4\pi }}\) und \(\Delta z \cdot \Delta {p_z} \ge \frac{h}{{4\pi }}\)
Konsequenzen der Unbestimmtheitsrelation
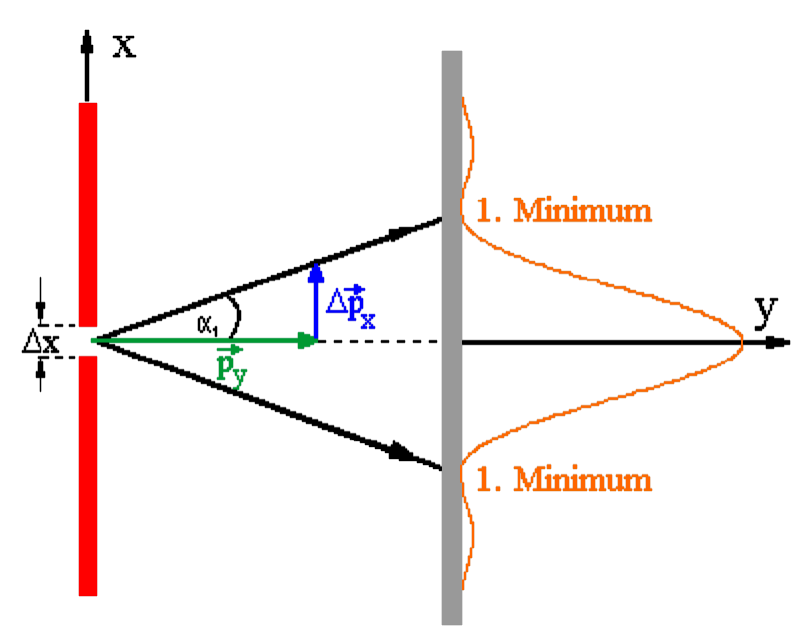
Eine einfache Ortsbestimmung eines Photonen- oder Elektronenbündels lässt sich mit einem Spalt (Spaltbreite \(\Delta x\)) machen.
Aus der nebenstehenden Simulation sieht man:
- Für einen breiten Spalt (große Ortsunbestimmtheit) ergibt sich eine relativ kleine Impulsunbestimmtheit (kleiner Öffnungswinkel des Bündels nach dem Spalt).
- Für einen schmalen Spalt (kleine Ortsunbestimmtheit) ergibt sich eine relativ große Impulsunbestimmtheit (großer Öffnungswinkel des Bündels nach dem Spalt).
Hinweis: Im Kapitel über die Interferenzerscheinungen beim Licht wurde im Wesentlichen der Doppelspalt und das Gitter behandelt. Interferenz tritt jedoch auch beim Einzelspalt auf. Hier sehen die Bedingungen für Maxima und Minima etwas anders aus.
Vor dem Spalt haben alle Quantenobjekte in dem Parallelbündel den Impulsbetrag py. Durch die Einengung auf den Ort \(\Delta x\) weitet sich das Bündel auf dem Weg zum Schirm auf. Die Quantenobjekte erhalten nun eine Unschärfe im Querimpuls, der im Folgenden abgeschätzt werden soll:
Der größte Teil der Quantenobjekte befindet sich innerhalb des Hauptmaximums der am Schirm entstehenden Beugungsfigur. Das Hauptmaximum ist durch die beiden Minima 1.Ordnung begrenzt.
Für das 1. Minimum bei der Beugung am Einzelspalt mit der Spaltbreite \(\Delta x\) gilt (anders als beim Doppelspalt)
\[\Delta x \cdot \sin \left( {{\alpha _1}} \right) = 1 \cdot \lambda \Leftrightarrow \sin \left( {{\alpha _1}} \right) = \frac{\lambda }{{\Delta x}}\]
Für den Zusammenhang zwischen Querimpuls und ursprünglichem Impuls gilt (vgl. Skizze)
\[\tan \left( {{\alpha _1}} \right) = \frac{{\Delta {p_x}}}{{{p_y}}}\]
Unter Berücksichtigung der Kleinwinkelnäherung (\(\sin \left( {{\alpha _1}} \right) \approx \tan \left( {{\alpha _1}} \right)\)) erhält man durch Gleichsetzen
\[\frac{{\Delta {p_x}}}{{{p_y}}} \approx \frac{\lambda }{{\Delta x}} \Leftrightarrow \Delta {p_x} \cdot \Delta x \approx {p_y} \cdot \lambda \quad(1)\]
Für die de BROGLIE-Wellenlänge \(\lambda \) gilt \(\lambda = \frac{h}{{{p_y}}}\). Setzt man dies in \((1)\) ein, so erhält man
\[\Delta {p_x} \cdot \Delta x \approx {p_y} \cdot \frac{h}{{{p_y}}} = h\]
Die hiermit gewonnene Unschärferelation stimmt zwar nicht ganz genau mit der von Heisenberg hergeleiteten überein. Dies ist aber nicht so entscheidend: wichtig ist nur die Erkenntnis, dass das Produkt aus den Unschärfen von Ort und Impuls nicht beliebig klein werden kann.
Diese Herleitung ergab auf der rechten Seite der Unbestimmtheitsrelation eine etwas andere Konstante. Dies ist aber nicht so entscheidend: wichtig ist nur die Erkenntnis, dass das Produkt aus den Unbestimmtheiten von Ort und Impuls nicht beliebig klein werden kann. Man kann also den Ort und den Impuls von Quantenobjekten gleichzeitig nicht beliebig genau bestimmen.
Diese Erkenntnis ist gleichbedeutend mit dem Abschied von der klassischen Bahnvorstellung bei Quantenobjekten, da die Beschreibung einer Bahn die gleichzeitige präzise Kenntnis von Ort und Impuls eines Objekts voraussetzt.
Diese Herleitung ergab auf der rechten Seite der Unbestimmtheitsrelation eine etwas andere Konstante. Dies ist aber nicht so entscheidend: wichtig ist nur die Erkenntnis, dass das Produkt aus den Unbestimmtheiten von Ort und Impuls nicht beliebig klein werden kann. Man kann also den Ort und den Impuls von Quantenobjekten gleichzeitig nicht beliebig genau bestimmen.
Diese Erkenntnis ist gleichbedeutend mit dem Abschied von der klassischen Bahnvorstellung bei Quantenobjekten, da die Beschreibung einer Bahn die gleichzeitige präzise Kenntnis von Ort und Impuls eines Objekts voraussetzt.
Aufgabe
Niels BOHR entwickelte das nach ihm benannte BOHRsche Atommodell. Nach BOHRs Vorstellung bewegt sich im Grundzustand des Wasserstoffatoms das Elektron auf einer Kreisbahn mit dem Radius \({r_e} = 0{,}53\cdot{10^{ - 10}}\rm{m}\) um den Kern. Die Geschwindigkeit des Elektrons auf dieser Kreisbahn beträgt \({v_e} = {\rm{ }}2{,}2\cdot{10^6}\rm{\frac{m}{s}}\).
Hinweis: Im Sinne der Quantenphysik ist diese Vorstellung von einer Elektronenbahn um den Kern nicht mehr zulässig, das Modell von BOHR also überholt. Trotzdem lieferten die Ansätze von BOHR sehr gute Ergebnisse bei der Deutung des Wasserstoffspektrums.
Bestimme mit Hilfe der HEISENBERGschen Unbestimmtheitsrelation die Unbestimmtheit in der Geschwindigkeit \(\Delta v\), wenn du von einer Ortsunbestimmtheit ausgehst, die dem Durchmesser der BOHRschen Bahn im Grundzustand entspricht.
Dauer und Genauigkeit
Außer der oben angegebenen Unbestimmtheitsrelation für Ort und Impuls gelten noch weitere Relationen ähnlichen Typs. Eine wichtige Unschärferelation besteht zwischen der Dauer \(\Delta t\) eines Vorgangs und der Genauigkeit \(\Delta E\), mit der die Energie der beteiligten Teilchen festgelegt ist:
\[\Delta E \cdot \Delta t \ge \frac{h}{{4\pi }}\]
Was bedeutet "unbestimmt"?
Ist eine Größe unbestimmt , dann ist es prinzipiell nicht möglich, einen exakten Wert zu benennen, egal wie genau gemessen werden kann.
Die Heisenbergsche Relation drückt eine solche objektiv gegebene Unbestimmtheit aus. Diese Unbestimmtheit von Ort und Impuls ist eine zentrale Eigenschaft der Quantenphysik. Das heißt also, dass es sich bei den Ausdrücken \(\Delta x\) und \(\Delta p\) nicht um Messungenauigkeiten handelt, sondern dass für diese Größen grundsätzlich kein genauer Wert bestimmt werden kann.
Hinweis: Manchmal wird die Heisenberg'sche Unbestimmtheitsrelation auch als Un-schärfe-relation bezeichnet. Der Begriff Unschärfe soll hier ebenfalls die grundsätzliche Unbestimmtheit der zu messenden Größe ausdrücken.