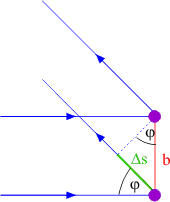
Für den Gangunterschied \(\Delta s\) gilt\[\Delta s = b \cdot \sin \left( \varphi \right)\quad (1)\]Für das Maximum 1. Ordnung gilt \(\Delta s=\lambda\). Setzt man dies in \((1)\) ein, so folgt\[\lambda = b \cdot \sin \left( \varphi \right)\quad (2)\]Für die Geschwindigkeit der - nicht relativistischen - Elektronen gilt\[\frac{1}{2} \cdot m \cdot {v^2} = {E_{{\rm{kin}}}} \Rightarrow v = \sqrt {\frac{{2 \cdot {E_{{\rm{kin}}}}}}{m}} \quad(3)\]Berechnung der Wellenlänge nach de BROGLIE:\[\lambda = \frac{h}{p} = \frac{h}{{m \cdot v}}\quad(4)\]Setzt man \((3)\) in \((4)\) ein, so folgt\[\lambda = \frac{h}{{\sqrt {2 \cdot m \cdot {E_{\rm{kin}}}} }}\quad (5)\]Setzt man \((5)\) in \((2)\) ein, so folgt\[{\frac{h}{{\sqrt {2 \cdot m \cdot {E_{{\rm{kin}}}}} }} = b \cdot \sin \left( \varphi \right) \Leftrightarrow \sin \left( \varphi \right) = \frac{h}{{b \cdot \sqrt {2 \cdot m \cdot {E_{{\rm{kin}}}}} }}}\]Einsetzen der gegebeben Werte liefert\[{\sin \left( \varphi \right) = \frac{{6,63 \cdot {{10}^{ - 34}}{\rm{Js}}}}{{2,15 \cdot {{10}^{ - 10}}{\rm{m}} \cdot \sqrt {2 \cdot 9,11 \cdot {{10}^{ - 31}}{\rm{kg}} \cdot 54 \cdot 1,60 \cdot {{10}^{ - 19}}{\rm{As}} \cdot {\rm{V}}} }} \approx 0,77 \Rightarrow \varphi \approx 51^\circ }\]