Ein Beispiel mit Hunden
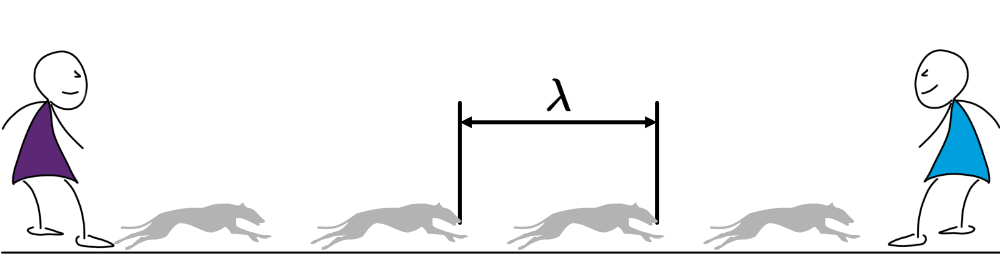
Sendet eine stehende Person A in konstanten Abständen von 10 Sekunden einen Hund der Geschwindigkeit \(c = 15\,{\rm\frac{m}{s}}\) zu einer 300 m entfernten Person B, so kommt der erste Hund nach 20 Sekunden an, die folgenden in 10 Sekunden-Abständen.
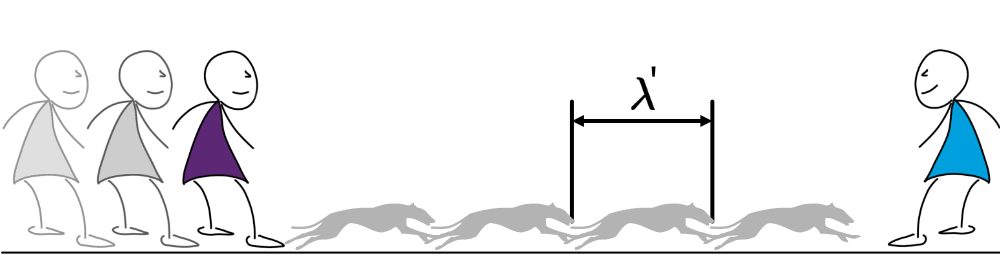
Sendet eine mit \(v = 3\,{\rm\frac{m}{s}}\) gehende Person A in konstanten Abständen von 10 Sekunden einen Hund der Geschwindigkeit \(c = 15\,{\rm\frac{m}{s}}\) zu einer 300 m entfernten stehenden Person B, so kommt der erste Hund nach 20 Sekunden an, der folgende hat einen 30 m kürzeren Weg, braucht also nur 18 Sekunden und kommt deshalb 8 Sekunden nach dem ersten an. Die Hunde kommen also in 8 Sekunden-Abständen.
Berechnung der veränderten Wellenlänge
Ein ruhender Sender der Frequenz \(f\) sendet eine Welle der Wellenlänge \(\lambda\) aus.
Dabei gilt \( \lambda = c \cdot T \) (T: Schwingungsdauer)
Beim einem sich mit der Geschwindigkeit \(v\) in Ausbreitungsrichtung bewegenden Sender verkürzt sich die Wellenlänge um \( \Delta \lambda = v \cdot T \),
so dass er die Wellenlänge \( \lambda' = \lambda - \Delta \lambda \) hat.
\[ \lambda' = \lambda - v \cdot T \Rightarrow v \cdot T = \lambda - \lambda' \Rightarrow v = \frac{\lambda - \lambda'}{T} \text{ oder } v = \frac{\lambda - \lambda'}{\lambda} \cdot c \]
Berechnung der veränderten Frequenz
Entsprechend ist auch die Frequenz verändert:
\[ \lambda' = \lambda \pm v \cdot T \text{ und } \lambda = c \cdot T \Rightarrow \lambda' = \lambda \pm v \cdot \frac{\lambda}{c} \Rightarrow \lambda' = \lambda \cdot \left(1 \pm \frac{v}{c}\right) \text{ und } f' = f \cdot \frac{1}{1 \pm \frac{v}{c}} \]
Merke
- Bewegt sich der Sender auf den Empfänger zu, wird die Wellenlänge kürzer, die Schwingungsdauer kleiner und die Frequenz größer (Blau – Verschiebung!)
- Bewegt sich der Sender vom Empfänger weg, wird die Wellenlänge größer, die Schwingungsdauer größer und die Frequenz kleiner (Rot – Verschiebung!)
Anwendung in der Astronomie
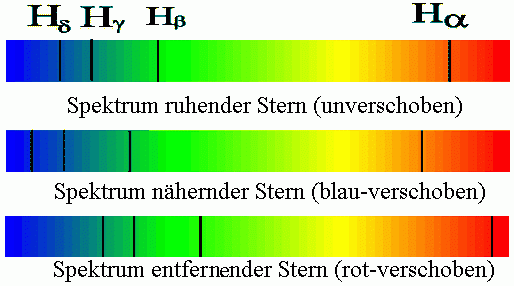
Am wichtigsten ist die Anwendung auf die Rot- und Blauverschiebung von Spektren, die man an der Verschiebung der typischen Absorptionslinien sieht. Dadurch kannst du bestimmen, ob sich ein Stern auf die Erde zubewegt, im Vergleich zur Erde in Ruhe ist oder sich von der Erde entfernt.