Der Sehwinkel beeinflusst die Bildgröße

Hält man ein 5-Cent-Stück in der Entfernung einer Armlänge vor das Auge, so erscheint das 5-Cent-Stück größer als der Vollmond.
Wie groß uns ein Gegenstand erscheint, hängt von der Größe des Netzhautbildes \(B\) ab und nicht von seiner tatsächlichen Größe. Das Netzhautbild wird durch den festen Abstand zwischen Augenlinse und Netzhaut und dem Sehwinkel \(\alpha\) bestimmt.
In der Skizze in Abb. 1 ist der betrachtete Gegenstand immer gleich groß. Von dem näher am Auge befindlichen Gegenstand wird jedoch ein größeres Bild \(\rm{B}_2\) auf deiner Netzhaut erzeugt. Der nahe Gegenstand erscheint unter dem größeren Sehwinkel \(\alpha_2\) und somit größer. Den weiter entfernten Gegenstand sehen wir unter dem kleineren Sehwinkel \(\alpha_1\). Daher erzeugt der weiter entfernte Gegenstand ein kleineres Bild \(\rm{B}_1\) auf der Netzhaut - du hast den Eindruck, dass der nahe Gegenstand größer ist als der weit entfernte.
Nahpunkt
Je geringer ein Gegenstand vom Auge entfernt ist, desto größer erscheint er dir. Jedoch sind der Annäherung Grenzen gesetzt: ab etwa 10cm Entfernung kann dein Auge nicht mehr auf den Gegenstand scharf stellen. Diesen Punkt bezeichnet man als Nahpunkt. Für dein Auge ist das jedoch sehr anstrengend. Die Entfernung, bei der das Scharfstellen (Akkommodieren) noch ohne große Anstrengung möglich ist, bezeichnet man als deutliche Sehweite, die häufig mit s bezeichnet wird. Sie beträgt ca. 25cm.
Definition der Vergrößerung
Man definiert die Vergrößerung \(V\) eines optischen Instrumentes ganz allgemein durch\[V = \frac{{{\alpha _{{\rm{mit}}}}}}{{{\alpha _{{\rm{ohne}}}}}}\;{\rm{d}}{\rm{.h}}{\rm{.}}\;{\rm{Vergrößerung}} = \frac{{{\rm{Sehwinkel}}\;{\rm{mit}}\;{\rm{Instrument}}}}{{{\rm{Sehwinkel}}\;{\rm{ohne}}\;{\rm{Instrument}}}}\]oder\[V = \frac{{{B_{{\rm{mit}}}}}}{{{B_{{\rm{ohne}}}}}}\;{\rm{d}}{\rm{.h}}{\rm{.}}\;{\rm{Vergrößerung}} = \frac{{{\rm{Größe}}\;{\rm{des}} \;{\rm{Netzhautbildes}} \;{\rm{mit}} \;{\rm{Instrument}}}}{{{\rm{Größe}} \;{\rm{des}} \;{\rm{Netzhautbildes}} \;{\rm{ohne}} \;{\rm{Instrument}}}}\]
Berechnung des Sehwinkels
Hinweis (nur für besonders Interessierte und weit Fortgeschrittene)
Zur Charakterisierung des Sehwinkels kann man anstelle des Winkels auch das Verhältnis \(\frac{G}{g}\) von Gegenkathete zu Ankathete in dem gelben rechtwinkligen Dreieck verwenden. Du wirst in einer späteren Klasse lernen, dass dieser Quotient mit dem Begriff Tangens (kurz: tan) abgekürzt wird.
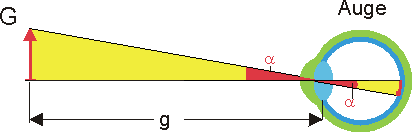
\[\tan \alpha = \frac{G}{g}\]Für die Vergrößerung \(V\) gilt dann\[V = \frac{{\tan {\alpha _m}}}{{\tan {\alpha _o}}}\]
Nahlupe
Eine Lupe ist eine einfache Sammellinse, deren Brennweite kleiner als die deutliche Sehweite ist (typische Werte: 20mm - 50mm). Die Nahlupe wird direkt vor das Auge gehalten, der zu betrachtende Gegenstand befindet sich in der Brennebene der Lupe. Somit sind die aus der Lupe tretenden Lichtstrahlen untereinander parallel und das Auge kann das Bild im völlig entspannten Zustand betrachten.
Hinweis: Hält man eine kleine Lupe direkt vor das Auge (dies tut z.B. der Uhrenmacher), so spricht man von einer Nahlupe. Darüber hinaus benutzt man große Lupen mit Handgriff, die weit entfernt vom Auge gehalten werden, um z.B. Details einer Landkarte zu bestimmen. Diese Lupen nennt man Leselupen.
Hinweis: Es ist auch g < f möglich. Dabei entsteht hinter der Lupe ein divergentes Bündel.
Im folgende Bild ist die Entstehung des Netzhautbildes ohne Lupe dargestellt (Gegenstand in deutlicher Sehweite s).
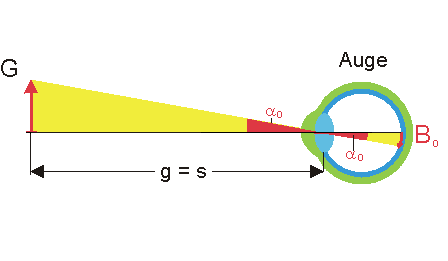
In der folgenden Animation kannst du die Konstruktion des Netzhautbildes bei Verwendung der Nahlupe nachvollziehen.
Vergrößerung einer Lupe
Für die Vergrößerung \(V_{\rm{Lupe}}\) einer Lupe mit der Brennweite \(f\) gilt\[V_{\rm{Lupe}} = \frac{s}{f}\]Dabei ist \(s\) die deutliche Sehweite des Menschen von ca. \(25\,\rm{cm}\).
Für besonders Fortgeschrittene zeigen wir auch die Herleitung der Formel für die Vergrößerung der Lupe.
Durch Vergleich des oberen mit dem unteren Bild kann man sich die Vergrößerung \(V\) der Lupe überlegen: Aus dem oberen Bild erkennt man\[\tan {\alpha _o} = \frac{G}{s}\]Aus der Animation kann man ablesen\[V = \frac{{\tan {\alpha _m}}}{{\tan {\alpha _o}}} = \frac{{\frac{G}{f}}}{{\frac{G}{s}}} \Rightarrow V = \frac{s}{f}\]


