Ziel eines jeden Fernrohres ist die Vergrößerung des Sehwinkels. Das von Johannes KEPLER (1571 - 1630) entwickelte KEPLER- oder astronomische Fernrohr besteht aus zwei Sammellinsen. Es entwirft ein höhen- und seitenverkehrtes Bild des Gegenstandes.
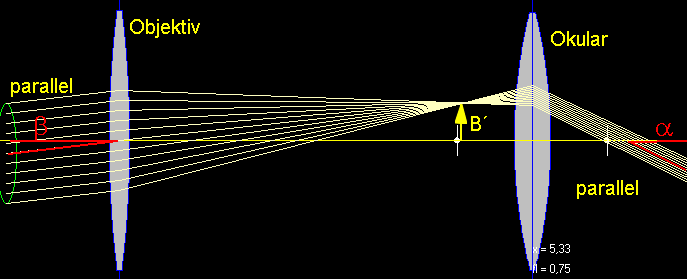
Wir gehen von einem sehr weit entfernten Gegenstand aus, dessen Sehwinkel \(\beta\) klein ist. Mit der ersten Sammellinse (Objektiv) wird zunächst ein reelles Zwischenbild \(B'\) erzeugt, das umso größer ist, je länger die Brennweite \(f_1\) des Objektivs ist.
Das reelle Zwischenbild wird mit einer als Lupe wirkenden Sammellinse (Okular) mit Brennweite \(f_2\)) betrachtet. Dabei fallen die Brennebenen von Objektiv und Okular zusammen. Somit ist die gesamte Baulänge des Kepler-Rohres \(l = f_1 + f_2\).
Für die Vergrößerung \(V\) des KEPLER-Fernrohres (der Vergrößerungsfaktor ist das Verhältnis des Winkels \(\alpha\) unter dem das Bild B´ mit Fernrohr auf die Augenlinse trifft zum Winkel \(\beta\) unter dem es ohne Linsen aufs Auge treffen würde) gilt \[V = \frac{{{B_m}}}{{{B_0}}}\] Mitteilung (ohne Beweis) \[\frac{{{B_m}}}{{{B_0}}} = \frac{{{f_1}}}{{{f_2}}} = \frac{{{f_{Objektiv}}}}{{{f_{Okular}}}}\] Es ist somit \[V = \frac{{{f_{Objektiv}}}}{{{f_{Okular}}}}\]
Die folgende Animation zeigt in einzelnen Schritten den Strahlengang durch das KEPLER-Fernrohr.
Für die Vergrößerung \(V\) des KEPLER-Fernrohres (der Vergrößerungsfaktor ist das Verhältnis des Winkels \(\alpha\) unter dem das Bild B´ mit Fernrohr auf die Augenlinse trifft zum Winkel \(\beta\) unter dem es ohne Linsen aufs Auge treffen würde) gilt \[V = \frac{{{B_m}}}{{{B_0}}}\] Mitteilung (ohne Beweis) \[\frac{{{B_m}}}{{{B_0}}} = \frac{{{f_1}}}{{{f_2}}} = \frac{{{f_{Objektiv}}}}{{{f_{Okular}}}}\] Es ist somit \[V = \frac{{{f_{Objektiv}}}}{{{f_{Okular}}}}\]
Hinweise
Durch den Einbau einer dritten Sammellinse kann man beim KEPLER-Fernrohr erreichen, dass das entworfene Bild höhen- und seitenrichtig ist, das Fernrohr also auch für Beobachtungen auf der Erde geeignet ist. Allerdings vergrößert sich dadurch die Baulänge weiter.
Man kann die Bildumkehr jedoch auch mit zwei totalreflektierenden Prismen erreichen, die - wenn man sie geschickt anordnet - auch noch eine geringere Baulänge des Fernrohrs (Prismenfernglas) zulassen.
Nur für besonders Interessierte und Fortgeschrittene
Betrachtet man das letzte Bild der Animation so kann man mit der Definition der Vergrößerung optischer Instrumente die Formel für die Vergrößerung des KEPLER-Fernrohres verstehen (Bz: Größe des reellen Zwischenbildes)\[V = \frac{{\tan {\alpha _m}}}{{\tan {\alpha _o}}}\quad da\quad \tan {\alpha _m} = \frac{{{B_z}}}{{{f_{Okular}}}}\quad und\quad \tan {\alpha _o} = \frac{{{B_z}}}{{{f_{Objektiv}}}}\quad {\rm{folgt}}\quad {\rm{V = }}\frac{{\frac{{{B_z}}}{{{f_{Okular}}}}}}{{\frac{{{B_z}}}{{{f_{Objektiv}}}}}}\quad \Rightarrow \quad V = \frac{{{f_{Objektiv}}}}{{{f_{Okular}}}}\]


