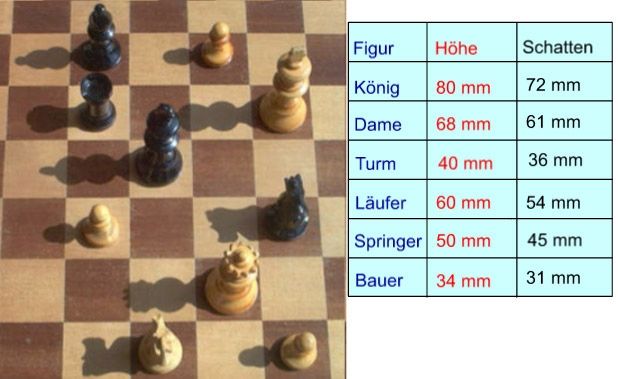
Nachweis direkter Proportionalität
Du siehst auf dem Schachbrett, dass je größer eine Schachfigur ist, desto länger ist ihr Schatten. Misst du bei jeder Figur die Höhe und die zugehörige Länge des Schattens, so erhältst du die neben dem Bild befindliche Messwerttabelle. Mithilfe der Tabelle kannst du nun auf unterschiedliche Art prüfen, ob zwischen Höhe der Figur und der Schattenlänge nur eine je - desto - Beziehung vorliegt oder ob diese Größen direkt proportional zueinander sind.
Prüfung auf mögliche direkte Proportionalität
Einen guten Hinweis (aber keinen "echten" Nachweis) auf direkte Proportionalität erhältst Du, wenn die Verdopplung von einem beliebigen Wert der Wertetabelle auch zu einer Verdopplung des zugehörigen Wertes führt. In unserem Schachspiel ist der Turm 40 mm hoch und sein Schatten ist 36 mm lang. Der König hat mit 80 mm gerade die doppelte Höhe des Turmes. Und mit einer Schattenlänge von 72 mm auch gerade die doppelte Schattenlänge. Es scheint hier also eine direkte Proportionalität vorzuliegen.
Nachweis durch Quotientengleichheit
| Höhe h in mm |
Schatten s in mm |
|
|---|---|---|
| 80 | 72 | 0,90 |
| 68 | 61 | 0,90 |
| 40 | 36 | 0,90 |
| 60 | 54 | 0,90 |
| 50 | 45 | 0,90 |
| 34 | 31 | 0,91 |
Zum Nachweis der direkten Proportionalität kannst du wie in der Tabelle den Quotienten zusammengehörender Größenpaare bilden. Sind diese Quotienten (im Rahmen der Messgenauigkeit) stets gleich, so sind die Größen direkt proportional. Mathematische bedeutet dies \[\frac{s_1}{h_1}=\frac{s_2}{h_2}=\frac{s_3}{h_3}\qquad \Rightarrow \qquad \frac{s}{h}=\rm{const.}\]
Grafischer Nachweis
Du kannst die Länge des Schattens und die Figurenhöhe auch wie in der Animation in Abb. 2 in ein passendes Koordinatensystem eintragen. Ergibt sich wie in diesem Beispiel eine Ursprungsgerade, so sind die Werte direkt proportional zueinander.
Hinweis: In der Animation in Abb. 2 wird unglücklicherweise die Schattenlänge auf der horizontalen und die Figurenhöhe auf der vertikalen Achse aufgetragen; besser sollte die Auftragung genau anders erfolgen, da die Figurenhöhe eher die unabhängige und die Schattenlänge die abhängige Größe darstellt.
Strahlensatz
Diese Form der Proportionalität bei Strahlenfiguren nennt man Strahlensatz. Du kannst den Strahlensatz sowohl bei Schatten als auch bei Lichtbündel oder bei der Lochkamera nutzen, da du immer ein Koordinatensystem so legen kannst, dass der Lichtstrahl eine Ursprungsgerade im x-y-System ist.
|
Schatten
|
Lichtbündel
|
Lochkamera
|
| \[\frac{h}{s} = const.\] | \[\frac{B}{g} = const.\] | \[\frac{B}{b} = const.\quad und\quad \frac{G}{g} = const.\] |
| \[\frac{{{h_1}}}{{{s_1}}} = \frac{{{h_2}}}{{{s_2}}}\] | \[\frac{{{B_1}}}{{{g_1}}} = \frac{{{B_2}}}{{{g_2}}}\] | \[\frac{B}{b} = \frac{G}{g}\] |